Zeah Engineering Factory

책 전반에서 살펴본 바와 같이, interconnection network의 설계는 성능 요구사항 명세와 몇 가지 패키징 및 비용 제약 조건으로부터 시작된다. 이러한 기준들이 해당 네트워크의 topology, routing, flow-control 선택을 이끈다. 이러한 설계 초기 결정들을 안내하기 위해, 우리는 zero-load latency와 throughput 같은 단순한 성능 예측 지표들을 소개했다. 물론 이 지표들은 네트워크에 대한 몇 가지 가정을 포함한다. 예를 들어, routing algorithm과 topology에 대한 대부분의 분석에서 이상적인 flow control을 가정했다. 네트워크 설계 초기에는 단순한 모델이 합리적이지만, 네트워크의 정확한 성능을 정확히 특성화하려면 더 정밀한 모델이 필요하다.

이 장에서는 먼저 네트워크의 기본적인 성능 지표들을 정의하고, 이 지표들을 어떻게 추정하고 해석하는지를 설명한다. 이어서 queuing model과 확률적 기법을 포함하는 상위 수준 네트워크 동작 모델링에 유용한 분석 도구들을 소개한다. 24장에서는 보다 정밀한 네트워크 시뮬레이터 사용을 다루고, 25장에서는 여러 네트워크 구성에서의 시뮬레이션 결과를 제시한다.

23.1 Interconnection Network 성능 측정 지표

특정 네트워크의 성능을 측정하고 표현하는 방법은 여러 가지가 있지만, 여기서는 throughput, latency, fault tolerance의 세 가지 기본 항목에 초점을 맞춘다. 이 용어들은 일반적으로 들릴 수 있으나, 그 정확한 정의는 어떻게 측정하느냐, 즉 측정 환경에 강하게 의존한다.

측정 구성

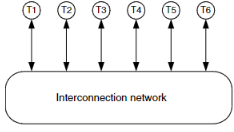
interconnection network의 표준 측정 구성은 그림 23.1에 나타나 있다. 네트워크 성능을 측정하기 위해, 네트워크의 각 terminal 또는 port에 terminal instrumentation을 부착한다. 이 instrumentation은 지정된 traffic pattern, packet 길이 분포, interarrival 시간 분포에 따라 packet을 생성하는 packet source를 포함한다. 각 terminal에서는 packet source와 네트워크 사이에 무한 깊이의 source queue가 존재한다. 이 source queue는 시뮬레이션 대상 네트워크의 일부는 아니며, traffic process와 네트워크를 분리하기 위해 사용된다. packet source와 source queue 사이에는 입력 packet을 카운트하고 각 packet의 시작 시간을 측정하는 input packet measurement process가 있다. 이 측정 프로세스는 반드시 source queue 이전에 위치해야 한다. 그래야 source에 의해 생성되었지만 아직 네트워크에 주입되지 않은 packet도 고려되며, packet의 latency가 source queue에서의 시간도 포함하게 된다. 각 출력 terminal에도 대응되는 측정 프로세스가 있어 packet을 카운트하고 각 packet의 종료 시간을 기록한다. throughput은 각 출력에서 도착한 packet을 카운트하여 측정하고, latency는 각 packet의 종료 시간에서 시작 시간을 뺀 값으로 측정한다.

Open-loop 측정

이러한 open-loop 측정 구성은 traffic parameter를 네트워크와 독립적으로 제어할 수 있게 해 준다. source queue가 없다면, packet source가 네트워크 terminal이 수용 불가능한 시점—예를 들어 input buffer가 가득 찼을 때—에 packet을 주입하려 할 수 있다. 이 경우, source가 생성한 traffic은 네트워크에 의해 영향을 받아 원래 지정한 traffic pattern이 아니게 된다. 우리는 일반적으로 특정 traffic pattern에서 네트워크를 평가하는 것이 목표이므로, throughput, latency, fault tolerance 측정을 위해 open-loop 방식을 사용한다.

Closed-loop 측정

네트워크가 traffic에 영향을 미치는 closed-loop 측정 시스템은 전체 시스템 성능을 측정할 때 유용하다. 예를 들어, multicomputer의 성능을 추정하려면 terminal instrumentation을 multicomputer processor 시뮬레이션으로 대체한 시뮬레이션을 수행한다. 생성되는 traffic은 실제 애플리케이션 실행 중 발생하는 프로세서 간 혹은 프로세서-메모리 간 메시지이다. 프로세서는 네트워크와 상호작용하므로 주입률은 쉽게 제어되지 않는다. 예를 들어, 메모리 응답을 기다리는 프로세서는 outstanding request 수 제한으로 인해 요청 수가 줄어든다. 이 설정에서는 보통 애플리케이션 실행 시간이 bandwidth, routing algorithm, flow control 같은 네트워크 parameter에 얼마나 민감한지 테스트하는 데 사용된다.

Steady-state 성능 측정

대부분의 경우, 우리는 네트워크의 정상 상태(steady-state) 성능, 즉 고정된 traffic source가 equilibrium에 도달한 후의 성능에 관심을 가진다. 네트워크가 equilibrium에 도달했다는 것은 평균 queue 길이가 정상 상태 값에 도달했다는 의미이다. 정상 상태 측정은 측정 대상 process가 stationary할 때만 의미 있다. 즉, process의 통계적 특성이 시간에 따라 변하지 않아야 한다. transient 성능 측정, 즉 traffic이나 구성 변화에 대한 네트워크의 응답도 때때로 관심 대상이지만, 대부분은 steady-state 측정에 초점을 둔다.

정상 상태 성능을 측정하기 위해 실험(또는 시뮬레이션)을 세 단계로 나눈다: warm-up, measurement, drain.

• Warm-up phase: 네트워크가 equilibrium에 도달할 수 있도록 N₁ 사이클을 실행하며, 이 기간 동안 packet은 측정되지 않는다.
• Measurement phase: N₂ 사이클 동안, source queue에 들어가는 모든 packet에 시작 시간이 태그되며, 이들을 measurement packet이라 부른다.
• Drain phase: measurement packet이 목적지에 모두 도달할 때까지 네트워크를 계속 실행한다. 도착한 packet의 종료 시간을 측정하고 기록한다. 이 측정 구간 동안 도착한 모든 packet은 throughput 측정을 위해 카운트된다. latency는 measurement packet의 시작 시간과 종료 시간으로 계산된다.

모든 measurement packet의 종료 시간을 측정하지 못하면 latency 분포의 꼬리 부분이 잘려 나가게 되므로, simulation을 충분히 길게 실행해야 한다.

※ 네트워크가 공정(fair)하지 않다면 마지막 measurement packet이 도달하는 데 많은 cycle이 걸릴 수 있다. 네트워크가 starvation에 취약하다면 drain phase가 끝나지 않을 수도 있다.

warm-up과 drain phase 동안에도 packet source는 packet을 계속 생성하지만, 이 packet은 측정 대상이 아니다. 그러나 이 packet은 background traffic으로서 measurement packet에 영향을 준다. N₁과 N₂ 값의 결정 방법은 24.3절에서 다룬다.

23.1.1 Throughput

Throughput은 특정 traffic pattern에서 네트워크가 packet을 전달하는 속도이다. 각 flow(즉, source-destination 쌍)에서 지정된 시간 동안 도착한 packet 수를 카운트하여 flow rate를 계산하고, 이로부터 전체 traffic pattern의 일부로서 얼마나 전달되었는지를 계산한다.

Throughput(accepted traffic)은 demand(offered traffic)과 대비된다. demand는 packet source가 packet을 생성하는 속도이다.

Throughput과 demand의 관계를 이해하기 위해 일반적으로 throughput(accepted traffic)을 demand(offered traffic)의 함수로 나타낸 그래프를 사용한다. (그림 23.2 참조) saturation 이하의 traffic 수준에서는 throughput이 demand와 같고, 이때 그래프는 직선이다. offered traffic이 계속 증가하면 결국 saturation에 도달하게 되며, 이는 throughput이 demand와 같게 유지되는 최대 수치이다. demand가 saturation을 넘으면 네트워크는 더 이상 동일한 속도로 packet을 전달할 수 없다.

packet이 생성되는 속도만큼 빠르게 전달되지 못하면 — 또는 적어도 우리가 요구하는 traffic pattern에 대해서는 — 네트워크는 saturation을 초과한 상태가 된다. saturation을 초과한 이후에도 안정적인 네트워크는 지정된 traffic pattern에 대해 최대 throughput을 유지하며 동작한다. 그러나 많은 네트워크는 불안정하며, saturation을 지나면 throughput이 급격히 떨어진다. 예를 들어, 그림 23.2의 네트워크는 안정적이며, saturation throughput은 전체 용량의 43%이다. 그림 23.3은 유사한 네트워크의 성능을 보여주는데, 이 또한 43%에서 saturation이 발생하지만, 그 이후 throughput이 급격히 하락하며 불안정하다. 이는 flow control mechanism의 unfairness 때문이며, 이러한 네트워크는 25.2.5절의 시뮬레이션 예제에서 더 자세히 분석된다.

throughput은 일반적으로 네트워크 용량의 일부로 표현된다. 이렇게 하면 네트워크의 성능을 더 직관적으로 이해할 수 있으며, 크기나 topology가 다른 네트워크 간의 비교도 가능하다. 예를 들어, 그림 23.2의 8-ary 2-mesh 네트워크의 총 용량은 U^,M=4b/k=b/2\hat{U},M = 4b/k = b/2U^,M=4b/k=b/2이다. 여기서 b는 channel bandwidth이다. 모든 source가 동일한 양의 traffic을 생성한다고 가정하면, 각 source는 bλ/2b\lambda/2bλ/2의 속도로 packet을 생성하며, 여기서 λ는 전체 용량 대비 offered traffic 비율이다. saturation은 이 용량의 43%에서 발생한다.

일부 불안정한 네트워크의 경우, saturation을 초과해도 전달된 packet의 총량은 일정하게 유지되지만, 이 packet들의 분포가 지정된 traffic pattern과 일치하지 않는다. 이러한 네트워크의 throughput을 정확히 측정하려면 특정 traffic pattern에 대한 throughput을 측정해야 한다. 이를 위해 네트워크의 모든 입력에 지정된 traffic을 적용하고, 각 flow에 대해 수용된 traffic을 별도로 측정한다. 지정된 traffic pattern에 대한 throughput은 모든 flow에 대해 수용된 traffic과 제공된 traffic의 비율 중 최소값으로 정의된다.

saturation을 초과하여 demand를 증가시키면, 도착지로 전달된 traffic matrix는 다음과 같은 형태를 가진다고 볼 수 있다:

즉, 목적지에 도달한 traffic은 우리가 원하는 traffic pattern의 Θ 단위와 추가적인 traffic X로 구성되며, X는 strictly positive한 행렬이다. throughput 측정 시 이 추가 traffic은 우리가 지정한 traffic pattern에 부합하지 않으므로 계산에 포함되지 않는다.

네트워크 불안정성은 종종 네트워크 내의 fairness 문제로 인해 발생한다. 과거에는 saturation 이후 평균 throughput만을 보고하는 경우가 많았으며, 이는 X에 대해 가산점을 주는 셈이다. 하지만 모든 flow 중 최소 throughput을 보고하면, 어떤 flow가 starvation되고 있는지를 확인할 수 있다. starvation은 일반적으로 unfair flow control의 결과이다. 그림 23.2에서는 saturation 이후에도 accepted traffic이 거의 일정하므로, 네트워크가 각 flow에 bandwidth를 공정하게 할당하고 있다고 볼 수 있다. 반면 그림 23.3에서는 saturation 이후 throughput이 급격히 감소하는데, 이는 flow control이 불공정하다는 것을 시사한다.

심지어 네트워크가 flow 간 bandwidth를 공정하게 할당하더라도, offered traffic이 증가함에 따라 accepted traffic이 줄어들 수 있다. 이는 non-minimal routing algorithm에 의해 발생할 수 있다. routing 결정이 불완전한 정보에 기반할 경우, contention이 증가하면서 misrouting도 늘어나고, 그 결과 packet이 더 많은 hop을 거치게 되어 channel load가 증가한다. 이러한 문제를 피하려면 routing algorithm을 신중히 설계해야 하며, 그렇지 않으면 saturation 이후 throughput이 빠르게 감소할 수 있다.

유사한 상황은 deadlock-free escape path를 사용하는 adaptive routing algorithm에서도 발생할 수 있다. offered traffic이 증가하면 더 많은 packet이 escape path로 밀려나고, accepted throughput은 결국 adaptive algorithm이 아닌 escape routing algorithm의 throughput 수준으로 떨어진다. 이 내용은 25.2절에서 추가로 다룬다.

offered traffic 대비 accepted traffic 그래프는 특정 traffic pattern에서 네트워크의 throughput 성능을 상세히 보여주지만, 여러 traffic pattern의 성능을 한눈에 보려면 saturation throughput에 대한 히스토그램을 그리는 것이 유용하다. 예를 들어, 10³ ~ 10⁶개의 무작위 permutation traffic pattern을 생성해 측정한 결과를 시각화할 수 있다. 이와 관련된 예시는 25.1절에 포함되어 있다.

23.1.2 Latency

Latency는 packet이 source에서 destination까지 네트워크를 통과하는 데 걸리는 시간이다. 지금까지 latency 평가는 주로 zero-load latency에 초점을 맞추었으며, 이는 shared resource에 대한 다른 packet들과의 contention에 의한 latency를 무시한다. contention latency를 모델링이나 시뮬레이션으로 포함하면 latency는 offered traffic의 함수가 되며, 이 함수를 그래프로 표현하면 도움이 된다. 그림 23.4는 latency vs. offered traffic 예시 그래프이다.

latency를 측정할 때는 그림 23.1의 측정 구성으로 traffic을 적용한다. 일반적으로 offered traffic αΛ를 α = 0에서 saturation throughput α = Θ까지 sweep한다. α > Θ인 traffic 수준에서는 latency가 무한대가 되어 측정이 불가능하다. 각 packet에 대해, source가 첫 번째 비트를 생성한 시점부터 마지막 비트가 네트워크를 빠져나가는 시점까지를 latency로 측정한다. 전체 latency는 모든 packet의 평균 latency로 보고된다. 경우에 따라서는 packet latency의 히스토그램, 최악의 packet latency, 특정 flow에 대한 통계도 유용하다. throughput과 마찬가지로 offered traffic은 네트워크 용량의 일부로 표시된다.

latency vs. offered traffic 그래프는 일정한 형태를 갖는다. 이는 zero-load latency의 수평 점근선에서 시작해, saturation throughput의 수직 점근선으로 향한다. low traffic 구간에서는 latency가 zero-load latency에 근접한다.

traffic이 증가함에 따라 contention도 증가하면서, packet은 buffer와 channel을 기다리게 되어 latency가 상승한다. 결국 offered traffic이 saturation throughput에 접근하면 latency 곡선은 수직 점근선에 근접하게 된다. 이 곡선의 형태는 기본적인 queuing theory (23.2.1절 참조)로 설명할 수 있다.

평균 latency도 유용하지만, 전체 또는 특정 subset에 대한 latency 분포를 분석하는 것도 의미 있다. 예를 들어, virtual-channel flow control을 사용하는 경우, 일부 채널은 high-priority traffic에 예약되어 있을 수 있다. 이럴 때 high-priority와 일반 traffic의 latency를 분리하여 분석하면 우선순위 정책의 효과를 평가할 수 있다. 또 하나의 유의미한 subset은 특정 source-destination pair 사이의 packet 전체이다. 특히 non-minimal routing algorithm을 사용하는 경우 유용하며, 해당 경로의 평균 길이를 추정하는 데 활용할 수 있다. 여러 latency 분포 그래프는 25.2절에 제시되어 있다.

23.1.3 Fault Tolerance

Fault tolerance는 하나 이상의 고장이 발생한 상태에서도 네트워크가 동작할 수 있는 능력을 의미한다. 네트워크의 fault tolerance에 대한 가장 중요한 정보는 고장 발생 시에도 정상적으로 동작할 수 있는지 여부이다. 어떤 node나 channel의 단일 고장이 있어도 (faulty terminal을 제외한) 모든 terminal 간 packet 전달이 가능한 경우, 해당 네트워크는 single-point fault tolerant하다고 한다. 많은 시스템에서는 단일 고장만 견딜 수 있어도 충분한데, 이는 단일 고장 확률이 낮고 동시에 여러 고장이 발생할 확률은 매우 낮기 때문이다. 또한 대부분의 고가용성 시스템은 고장이 발생하면 즉시 복구되므로 다른 고장이 발생하기 전에 faulty component가 교체된다.

fault tolerance 요구는 여러 설계 결정에 영향을 준다. 예를 들어, 네트워크가 single-point fault tolerant해야 한다면 deterministic routing을 사용할 수 없다. 특정 channel에 fault가 생기면, 그 경로를 사용하는 모든 node pair가 연결을 잃기 때문이다. fault가 발생해도 성능이 점진적으로 저하된다면, 이를 graceful degradation이라고 부른다. fault-tolerant 네트워크의 성능은 25.3절에서 다룬다.

23.1.4 Common Measurement Pitfalls

interconnection network의 성능을 측정할 때 자주 발생하는 오류가 몇 가지 있다. 저자들 자신도 과거에 이러한 실수를 저질렀으며, 여기에서 소개함으로써 독자들이 같은 실수를 반복하지 않기를 바란다.

Source queue 누락: 네트워크 성능을 측정하면서 source queue를 제대로 구성하지 않는 경우가 많다. 그림 23.5는 source queue의 효과가 누락되는 두 가지 경우를 보여준다. 그림 23.5(a)에서는 아예 source queue가 없다. 이 경우...

그림 23.5 설명

그림 23.5는 무한한 source queue 없이 네트워크 성능을 측정하려는 시도를 보여준다. 결과 시스템은 closed loop가 되며, 적용된 traffic pattern은 원래 의도한 패턴이 아니게 되고, 측정된 latency는 네트워크 진입을 대기한 시간을 포함하지 않는다.

• (a): 입력 채널이 바쁠 때 source는 packet을 drop하거나 입력이 가능해질 때까지 injection을 지연시켜야 한다. 후자의 경우, 이후 packet의 생성도 지연되어야 하며, 그렇지 않으면 queue가 필요하다. 어느 경우든 네트워크의 contention이 traffic pattern에 영향을 주게 된다.
• (b): source queue는 존재하지만, packet 카운팅과 timing이 source queue의 출력에서 시작된다.

source queue가 없이 수행된 측정은 두 가지 이유로 무효이다.
첫째, 측정 지점에서 적용된 traffic pattern이 우리가 의도한 것과 다르다. 예를 들어 그림 23.6의 간단한 두 노드 네트워크를 보자. 여기서 node 1에서 0으로, 그리고 0에서 1로 각각 1 단위의 traffic을 주입하도록 설정한다. 그러나 source queue 출력 이후에서 packet을 측정하면, 실제 routing에 수락된 0 → 1 방향의 0.1 단위 traffic만 카운트되며, 반대 방향은 전체 1 단위가 그대로 측정된다. 이 결과는 우리가 측정하고자 하는 traffic pattern이 아니다.

둘째, source queue를 생략하면 packet latency가 과소 추정된다. queue 깊이가 얕고 blocking flow control을 사용하는 네트워크에서는 고부하 상황에서 발생하는 contention latency의 대부분이 source queue에서 발생한다. 실제로 네트워크 내부로 packet이 들어가면, 빠르게 전달되는 경우가 많다. 입력 채널을 기다리는 시간을 제외하면 실제 latency보다 훨씬 낮은 값이 측정된다.

평균 throughput만 보고하는 문제

입력 측정에서는 source queue 생략이 문제였다면, 출력 측정에서는 flow별 최소 throughput이 아닌 평균 throughput을 보고하면 문제가 된다. 이 경우에도 실제 측정 대상 traffic pattern과 다른 결과가 나온다.

예를 들어 그림 23.6의 네트워크를 보자. 두 목적지에 도달한 traffic의 평균을 내면, 1과 0.1의 평균인 0.55 단위에서 saturation이 일어난다고 결론 내릴 수 있다. 그러나 실제로 네트워크는 아래와 같이 전달하고 있다:

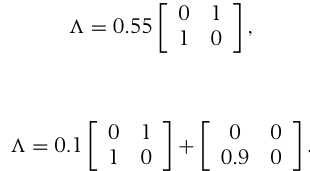
즉, 지정된 traffic pattern의 0.1 단위만 전달되고 나머지는 추가 traffic일 뿐이다. flow 중 최소 수용량을 측정해야 정확한 throughput을 알 수 있다.

특정 flow가 starvation되는 네트워크에서는 평균 throughput만 보고하면 이러한 문제가 완전히 감춰진다. 예를 들어 chaotic routing에서는 네트워크 내부의 packet에 절대적인 우선권을 부여하므로, 일부 input에서는 네트워크가 바쁠 경우 packet이 전혀 진입하지 못해 완전히 starving될 수 있다. 이때 평균 throughput은 여전히 높게 유지되므로, 네트워크가 안정적인 것처럼 보이지만 실제로는 일부 flow가 완전히 차단된 불안정한 상태다.

Latency와 throughput을 함께 나타내는 그래프

일부 연구자는 latency vs. offered traffic 곡선과 accepted vs. offered traffic 곡선을 하나의 그래프로 표현하려 한다. 그림 23.7이 그 예시이다. 이 그래프는 latency를 accepted traffic의 함수로 나타내며, 곡선 위의 각 점은 offered traffic의 다양한 수준을 나타낸다. 불안정한 네트워크에서는 accepted traffic이 saturation 이후 감소하기 때문에, 곡선이 왼쪽으로 되돌아가는 모양을 보인다.

이런 형태의 가장 큰 문제점은 source queue가 측정에 포함되지 않았다는 것을 드러낸다는 점이다. source queue를 고려했다면, saturation을 초과한 모든 offered traffic에서 latency는 무한대가 되어야 하며, 곡선은 wrap-around되지 않고 최대 accepted traffic에서 점근선 형태로 끝나야 한다.

게다가 BNF(Burton Normal Form) 차트는 일반적으로 steady-state 성능을 반영하지 않는다. 대부분의 불안정한 네트워크에서는 saturation 직후 accepted traffic이 급격히 낮아진 후, 그 이후 offered traffic이 증가해도 그 수준에 머문다. 이는 saturation 이후 source queue가 무한히 커지기 시작하기 때문이며, steady-state에서는 큐 크기가 고정된 것이 아니라 무한이 된다. BNF 차트에서 gradual fold-back이 보인다면, simulation이 충분히 오래 실행되지 않았다는 뜻이다.

테스트 구간 동안 생성된 모든 packet을 측정하지 않은 경우

간혹 목적지에서 수신된 packet들의 latency 평균만을 측정하는 경우가 있는데, 이는 측정 구간 동안 생성된 모든 packet을 측정한 것이 아니므로 오류다. 이 경우 긴 latency를 가진 packet들은 측정에 포함되지 않아 latency 분포의 꼬리 부분이 잘리고 평균 latency도 과소 추정된다. warm-up 이후 생성된 packet의 unbiased 샘플을 사용해야 한다. arrival 기준으로 선택한 packet은 편향된 샘플이다.

무작위 traffic만 사용하는 문제

Uniform random traffic은 네트워크 채널 간 load를 자연스럽게 균등하게 분산시켜주는 아주 benign한 패턴이다. nearest-neighbor traffic보다는 약하지만, 거의 best-case workload에 가깝다. 이 때문에 좋지 않은 routing algorithm조차 무난하게 보이게 할 수 있다. 따라서 다양한 adversarial traffic pattern (3.2절 참조)과 충분히 많은 무작위 permutation을 함께 사용해야 한다.

23.2 Analysis

interconnection network의 성능을 측정하기 위해 여러 도구들이 존재한다. 분석(analysis), 시뮬레이션(simulation), 실험(experiment) 모두 네트워크 평가에서 중요한 역할을 한다.

우리는 일반적으로 수학적 모델을 통해 네트워크 성능을 추정하는 분석으로부터 시작한다. 분석은 적은 노력으로 근사적인 성능 수치를 제공하며, 다양한 요소들이 성능에 어떻게 영향을 미치는지를 파악할 수 있게 해 준다. 또한, 분석을 통해 다양한 파라미터나 설정을 가진 네트워크 전체에 대한 성능 예측을 할 수 있는 수식 집합을 도출할 수 있다.

하지만 분석은 보통 여러 가지 근사나 가정을 포함하게 되므로 결과의 정확도에 영향을 줄 수 있다.

분석을 통해 근사적인 결과를 얻은 후에는 보통 시뮬레이션을 수행하여 분석 결과를 검증하고 보다 정확한 성능 추정을 얻는다. 좋은 모델을 사용할 경우 시뮬레이션은 정확한 성능 예측을 제공하지만, 그만큼 시간이 많이 소요된다. 각 시뮬레이션 실행은 단일 네트워크 구성, traffic pattern, load point만 평가할 수 있다. 또한 시뮬레이션은 결과만 요약해서 보여주므로, 어떤 요인이 성능에 영향을 주었는지 직접적인 통찰을 제공하지는 않는다.

※ 하지만 적절한 instrumentation을 사용할 경우, 시뮬레이션을 통해 성능 문제를 진단할 수도 있다.

router의 타이밍과 arbitration을 무시하는 시뮬레이터는 정확도가 매우 낮은 결과를 낼 수 있다.
네트워크가 실제로 구축된 후에는, 실험을 통해 실제 성능을 측정하고 시뮬레이션 모델을 검증한다. 물론 이 시점에서 성능 문제가 발견되면 수정하기 어렵고, 시간과 비용이 많이 든다.

이 절에서는 네트워크 성능 평가의 첫 번째 단계인 분석(analysis)을 다룬다. 특히, analytic performance analysis를 위한 두 가지 기본 도구인 queuing theory와 probability theory를 소개한다. queuing theory는 packet이 대부분의 시간을 큐에서 대기하는 네트워크 분석에 유용하고, probability theory는 contention 시간이 주로 blocking에 의해 발생하는 경우에 적합하다.

23.2.1 Queuing Theory

interconnection network에서 packet은 많은 시간을 큐에서 대기하며 보낸다. 측정 구성에서의 source queue뿐 아니라, 경로상 각 단계의 input buffer들도 큐로 간주된다. queuing theory를 이용하여 각 큐에서 packet이 대기하는 평균 시간을 예측함으로써, packet latency의 구성 요소들을 근사할 수 있다.

queuing theory 전체를 다루는 것은 이 책의 범위를 넘지만, 이 절에서는 queuing theory의 기본 개념을 소개하고 이를 단순한 interconnection network 분석에 어떻게 적용할 수 있는지 설명한다. 보다 자세한 내용은 queuing theory 전문 서적 [99]을 참고하라.

그림 23.8은 기본적인 큐잉 시스템을 보여준다.

source는 초당 λ개의 packet을 생성한다. 이 packet들은 service를 기다리며 큐에 저장된다. server는 큐에서 순차적으로 packet을 꺼내 평균 T초의 시간 동안 처리하며, 평균 처리율은 μ = 1/T packet/초이다.

interconnection network에서의 packet source는 terminal에서 packet을 주입하거나 다른 node로부터 packet을 전달하는 channel이다. arrival rate λ는 input terminal에서 들어오는 traffic rate이거나, 네트워크 channel에 들어오는 traffic의 superposition일 수 있다. server는 네트워크에서 packet을 제거하는 terminal이거나, packet을 다른 node로 운반하는 channel이다. 두 경우 모두 service time T는 packet이 channel 또는 terminal을 통과하는 시간이며, packet 길이에 비례하므로 T = L/b로 표현된다.

Markov Chain을 이용한 모델링

분석을 단순화하기 위해, 우리는 현실과 다르다는 것을 알고 있으면서도 몇 가지 가정을 한다.

• 큐는 무한 길이를 가진다고 가정
• packet 간 도착 시간(inter-arrival time)과 service time은 exponential distribution을 따른다고 가정

exponential process는 memoryless라고도 하며, 새 이벤트(예: packet 도착)가 발생할 확률이 과거 이벤트에 영향을 받지 않는다. arrival과 service를 이렇게 단순화하면, queuing system을 Markov chain으로 모델링할 수 있다 (그림 23.9 참조).

그림 23.9의 Markov chain은 큐의 상태 전이를 나타낸다. 각 원은 큐의 상태를 나타내며, 해당 상태에서 큐에 존재하는 packet 수로 라벨링된다. packet은 λ의 속도로 큐에 도착하고, 이에 따라 상태는 오른쪽으로 전이된다. 반대로 packet이 큐에서 제거되면 μ의 속도로 왼쪽 상태로 전이된다.

정상 상태에서는 어떤 상태로 들어오는 속도와 나가는 속도가 같아야 한다.
예를 들어 상태 p₀에 대해서는 다음과 같다:

기대 queue 길이 및 대기 시간

각 상태의 확률을 구했으므로, 큐에 있는 평균 entry 수(기대 queue 길이)는 다음과 같다:

E(NQ)=∑i=0∞ipi=ρ/(1−ρ)E(N_Q) = ∑_{i=0}^{∞} i p_i = ρ / (1 - ρ)E(NQ​)=i=0∑∞​ipi​=ρ/(1−ρ)

즉, 도착한 packet은 앞서 있는 packet들을 기다려야 하므로 평균 대기 시간은 다음과 같이 계산된다:

E(TW)=T×E(NQ)=Tρ/(1−ρ)=ρμ(1−ρ)E(T_W) = T × E(N_Q) = Tρ / (1 - ρ) = \frac{ρ}{μ(1 - ρ)}E(TW​)=T×E(NQ​)=Tρ/(1−ρ)=μ(1−ρ)ρ​

이 관계는 Little's law로 알려져 있다.

분산 및 다른 queue 유형

queue entry 수의 분산(variance)은 다음과 같다:

Var(NQ)=E(σNQ2)=ρ/(1−ρ)2Var(N_Q) = E(σ^2_{N_Q}) = ρ / (1 - ρ)^2Var(NQ​)=E(σNQ​2​)=ρ/(1−ρ)2

우리는 지금 M/M/1 queuing system에 대해 계산하였다. 이는 도착 및 서비스 시간이 exponential distribution을 따르며 server가 1개인 시스템이다.

다음은 기타 queue 유형과 비교한 결과:

• M/D/1 (deterministic service time)의 경우:

E(NQ)=ρ2(1−ρ)E(N_Q) = \frac{ρ}{2(1 - ρ)}E(NQ​)=2(1−ρ)ρ​

• M/G/1 (general service time)의 경우:

E(NQ)=λ2X22(1−ρ)E(N_Q) = \frac{λ^2 X^2}{2(1 - ρ)}E(NQ​)=2(1−ρ)λ2X2​

여기서 X²는 service time의 두 번째 모멘트이다. 많은 네트워크에서는 packet 길이, 즉 service time이 일정하거나 거의 일정하기 때문에, 일반적으로 위 식 (23.8) 또는 (23.9)를 사용하는 것이 식 (23.5)보다 더 적절하다.

주의할 점은, λ ≥ μ 또는 ρ ≥ 1인 경우 위 식들이 무효라는 것이다. 이때 latency는 무한이 되며, 위 식들은 음수를 반환하므로 적용할 수 없다.

네트워크 모델 예시: Butterfly Network

그림 23.10은 queuing theory를 사용하여 4-terminal butterfly network를 모델링하는 예를 보여준다.

• (a): 2-ary 2-fly 네트워크가 uniform traffic을 전달
• (b): 이를 queuing system으로 모델링

각 source는 λ 속도의 packet stream을 생성하는 source로, 각 destination은 service rate μ를 가지는 server로 모델링된다.

각 2×2 switch는 splitter(입력), combiner(출력), 그리고 output queue 두 개로 구성된다.

• splitter는 λ rate의 입력을 λ/2씩 나누어 각 switch 출력으로 보낸다.
• 각 combiner는 입력 두 개로부터 λ/2 stream을 받아 λ rate로 output queue로 전달한다.

각 switch의 output queue는 combiner에 의해 합쳐진 traffic을 받아들인다. 이 큐는 내부 채널에 의해 μc 속도로 서비스되며, 마지막 단계에서는 terminal에 의해 μ 속도로 서비스된다.

이러한 switch model은 Poisson arrival process의 특성을 활용한다. 즉, exponential inter-arrival time을 갖는 stream을 나누면 여전히 exponential 특성을 유지하는 stream들이 생성된다.

23.2.2 Probabilistic Analysis

queuing theory를 보완하기 위해, 우리는 probabilistic analysis를 사용하여 buffer가 없는 네트워크 또는 네트워크 구성 요소를 분석한다.

Section 2.6에서 dropping flow control이 적용된 네트워크의 성능을 추정하기 위해 probabilistic analysis를 사용한 예제를 이미 살펴본 바 있다. 이 절에서는 blocking flow control을 사용하는 네트워크의 성능을 어떻게 추정하는지 보여준다.

예를 들어, 그림 23.12(a)와 같은 blocking flow control과 queuing이 없는 2×2 switch를 생각해 보자. 각 출력 포트의 service time은 같고, deterministic하며, To로 설정한다. 두 입력의 traffic rate는 동일하며, λ₁ = λ₂ = λ이고, 양쪽 입력에서 나오는 traffic은 두 출력에 대해 균일하게 분포되어 있다고 가정한다. 즉, λᵢⱼ = λ / 2 (∀i, j).

i₁ 입력 채널이 바쁜(busy) 시간 Ti를 계산하기 위해, 먼저 i₁에 들어온 packet이 대기해야 할 확률 Pw를 계산한다:

Pw=λTo2=ρo2P_w = \frac{λ T_o}{2} = \frac{ρ_o}{2}Pw​=2λTo​​=2ρo​​

여기서 ρₒ = λ To 는 출력 링크의 duty factor이다.

packet이 대기해야 하는 경우, 평균 대기 시간 Twc는 다음과 같다:

Twc=To2T_{wc} = \frac{T_o}{2}Twc​=2To​​

이를 종합하면, 전체 packet에 대한 평균 대기 시간 Tw는:

Tw=PwTwc=λTo24=ρoTo4T_w = P_w T_{wc} = \frac{λ T_o^2}{4} = \frac{ρ_o T_o}{4}Tw​=Pw​Twc​=4λTo2​​=4ρo​To​​

결국 입력 채널의 busy 시간 Ti는 다음과 같다:

Ti=To+Tw=To(1+λTo4)=To(1+ρo4)T_i = T_o + T_w = T_o \left(1 + \frac{λ T_o}{4} \right) = T_o \left(1 + \frac{ρ_o}{4} \right)Ti​=To​+Tw​=To​(1+4λTo​​)=To​(1+4ρo​​)

이 식은 switch의 입력 측 busy 시간이 출력 링크의 duty factor에 비례해 증가함을 보여준다.

collision이 발생했을 때의 대기 시간 Twc는 service time의 분산에 큰 영향을 받는다. deterministic한 service time의 경우, 평균적으로 packet은 이미 처리 중인 packet의 중간 지점에서 도착하므로 Twc = To / 2가 된다. 만약 service time이 exponential 분포를 따른다면, 기대 대기 시간은 두 배로 증가하여:

Twc=To,Tw=λTo22=ρoTo2,Ti=To(1+ρo2)T_{wc} = T_o, \quad T_w = \frac{λ T_o^2}{2} = \frac{ρ_o T_o}{2}, \quad T_i = T_o \left(1 + \frac{ρ_o}{2} \right)Twc​=To​,Tw​=2λTo2​​=2ρo​To​​,Ti​=To​(1+2ρo​​)

이처럼 service time의 분산이 커지면 대기 시간도 증가한다. 이는 긴 service time을 가진 packet들이 전체 busy 시간에서 더 많은 비율을 차지하기 때문이다. multistage network를 분석할 때는 각 단계마다 분산이 다를 수 있다. 예를 들어, 그림 23.12의 switch는 deterministic한 출력 service time을 갖지만, 여전히 non-zero variance를 가진다.

23.3 Validation

queuing theory, probabilistic analysis, 또는 simulation이 interconnection network의 성능을 얼마나 정확하게 예측할 수 있는지는 해당 분석에서 사용한 모델의 정확도에 달려 있다.

모델이 네트워크의 모든 관련 동작을 정확하게 반영한다면, 분석은 매우 정확해질 수 있으며, 넓은 설계 공간을 빠르게 탐색하거나 성능에 영향을 주는 요인을 이해하는 데 강력한 도구가 될 수 있다. 반면, 중요한 네트워크 특성을 누락하거나 부적절한 근사치를 사용하면 실제 네트워크 성능과 크게 다른 결과가 나올 수 있다. 시뮬레이션도 마찬가지로, 부정확한 모델은 부정확한 결과를 낳는다.

Validation은 analytic model 또는 simulation model이 실제로 정확한지를 검증하는 과정이다. 예를 들어, 실제 네트워크에서 측정한 latency vs. offered traffic 데이터를 보유하고 있다면, 이를 사용해 simulation 또는 analysis 결과와 비교해 볼 수 있다. 결과가 일치하면 해당 모델이 중요한 요소들을 정확히 반영하고 있다고 판단할 수 있으며, 유사한 네트워크나 조건에서도 정확할 가능성이 높다.

실험 데이터가 없는 경우, 신뢰할 수 있는 simulation 결과를 기준으로 analytic model을 검증할 수도 있다. 그림 23.11은 이런 방식의 validation 예시다.

모델을 검증하려면 다양한 동작 지점과 네트워크 구성에서의 결과를 대표적인 데이터와 비교해야 한다. 특정 하나의 지점에서 모델이 정확하다고 해서, 매우 다른 조건에서도 정확할 것이라고 단정할 수는 없다. 예를 들어, zero-load latency를 정확히 예측한다고 해서 saturation 근처의 latency를 정확히 예측한다고 보장할 수는 없다.

23.4 사례 연구: BBN Monarch Network의 효율성과 손실

BBN Advanced Computer Systems는 Butterfly TC-2000 (Section 4.5)을 계승한 시스템으로 BBN Monarch [156]를 설계했다. Monarch는 많은 흥미로운 구조적 특징을 포함하고 있었지만, 결국 완성되지 못했다.

Monarch는 uniform-memory-access shared memory 시스템이었다. 최대 64K개의 processor가 butterfly-like 네트워크를 통해 N개의 memory module에 접근했다. 이 네트워크는 다음과 같은 특징을 가지고 있었다:

• dropping flow control 사용
• 목적지 memory module을 무작위화하기 위한 hashed memory address
• hot-spot traffic 처리를 위한 access combining 기법

접근은 동기적(synchronous)으로 이루어졌는데, 이는 combining을 단순화하기 위한 목적이었다. 시간은 frame으로 나뉘며, 각 processor는 frame 시작 시 1회의 memory access를 수행할 수 있었다. 같은 frame 내에서 같은 위치로 접근하는 요청들은 네트워크 내부 노드에서 결합(combine) 되어 단일 access packet으로 memory module로 전달되었다.

Monarch 네트워크는 그림 23.13과 같이 switch와 concentrator 단계를 번갈아 배치하여 구성되었다.

• 각 switch는 최대 12개의 입력과 32개의 출력을 가졌으며, 최대 4비트의 주소를 해석할 수 있었다.
• switch의 출력 포트는 그룹 단위로 구성되어, 같은 방향으로 여러 packet이 동시에 전송될 수 있도록 했다.
  예를 들어, 하나의 switch는 2포트씩 16개의 출력 그룹, 또는 4포트씩 8개의 출력 그룹으로 구성할 수 있었다.

packet은 switch의 어떤 입력 포트로 도착하든, 구성된 출력 그룹 내의 어떤 포트를 통해도 전송이 가능했다.

그림 23.13에 보이는 BBN Monarch 네트워크(1990)는 switch와 concentrator를 번갈아 배치한 stage들로 구성되어 있다. 각 stage에서의 concentration ratio는 효율성을 극대화하고 dropping flow control로 인한 손실을 최소화하기 위해 조정되었다. 각 채널은 직렬(serial) 방식으로 작동하며, 대역폭은 350 Mbit/s였다.

각 packet은 요청한 출력 그룹의 어느 채널이든 하나를 얻을 수 있으면 다음 stage로 진행했다. 그렇지 못하면 drop되었다.

Concentrator는 여러 개의 lightly loaded 채널을 더 적은 수의 heavily loaded 채널로 multiplexing하는 역할을 한다. 예를 들어, 여러 패키징 단계를 거쳐야 하는 고비용 채널 전에 이를 사용하는 방식이다.

• 각 concentrator 칩은 최대 32개의 입력과 12개의 출력을 지원한다.
• 모든 입력과 출력은 동등하며, 매 frame마다 32개 입력 중 어떤 12개에서든 도착한 최대 12개의 packet만이 출력으로 라우팅된다.
• 추가로 도착한 packet은 drop된다.

손실 확률 계산

probabilistic analysis를 이용하여 Monarch 네트워크 각 단계에서의 packet 손실 확률을 계산할 수 있다. 다음의 가정을 사용한다:

• 모든 입력 채널은 균일하게 load됨
• traffic은 출력에 대해 균일하게 분포됨
• address hashing과 access combining이 이 가정을 현실적으로 만들어 줌

어떤 switch가 I 개의 입력, G 개의 출력 그룹, 그리고 각 그룹당 C개의 채널을 가질 때, 입력 duty factor가 Pi라고 하자. 특정 입력 i가 특정 출력 그룹 j를 요청할 확률은 다음과 같다:

Pij=PiGP_{ij} = \frac{P_i}{G}Pij​=GPi​​

이때, k개의 입력이 같은 출력 j를 요청할 확률은 이항 분포를 따른다:

Pk=(Ik)(PiG)k(1−PiG)I−kP_k = \binom{I}{k} \left( \frac{P_i}{G} \right)^k \left( 1 - \frac{P_i}{G} \right)^{I - k}Pk​=(kI​)(GPi​​)k(1−GPi​​)I−k

출력 채널 j가 busy할 확률 Po는, k ≤ C인 경우에 대해 다음과 같이 계산된다.
k개의 요청 중 (C - k)/C 비율만큼은 채널이 idle이므로:

Po=1−∑k=0C−1(C−kC)PkP_o = 1 - \sum_{k=0}^{C-1} \left( \frac{C - k}{C} \right) P_kPo​=1−k=0∑C−1​(CC−k​)Pk​

이를 정리하면:

Po=1−∑k=0C−1(C−kC)(Ik)(PiG)k(1−PiG)I−k(23.14)P_o = 1 - \sum_{k=0}^{C-1} \left( \frac{C - k}{C} \right) \binom{I}{k} \left( \frac{P_i}{G} \right)^k \left( 1 - \frac{P_i}{G} \right)^{I - k} \tag{23.14}Po​=1−k=0∑C−1​(CC−k​)(kI​)(GPi​​)k(1−GPi​​)I−k(23.14)

효율성과 손실 계산

각 단계의 efficiency는 출력 traffic의 총합을 입력 traffic의 총합으로 나눈 값이다:

P(transmit)=GCPoIPi(23.15)P(\text{transmit}) = \frac{G C P_o}{I P_i} \tag{23.15}P(transmit)=IPi​GCPo​​(23.15)

손실률은 다음과 같다:

P(drop)=1−P(transmit)=1−GCPoIPi(23.16)P(\text{drop}) = 1 - P(\text{transmit}) = 1 - \frac{G C P_o}{I P_i} \tag{23.16}P(drop)=1−P(transmit)=1−IPi​GCPo​​(23.16)

표 23.1은 64K 포트를 갖는 Monarch 네트워크의 구성과 손실 분석 결과를 보여준다.
각 stage마다 식 (23.14)를 사용해 Po를 계산하고, 이 값을 다음 단계의 Pi로 사용하여 efficiency 및 손실률을 계산한다.

결과적으로 이 네트워크는 100% input load에서도 손실률 10% 미만을 달성할 수 있다.
단, 그 대가로 링크를 과도하게 구성하여 각 switch의 입력은 65% 미만, 각 concentrator의 입력은 25% 미만만 사용하도록 설계되었다. 이와 관련된 duty factor와 loss 간의 관계는 연습문제 23.7에서 탐구한다.

버퍼링의 영향

버퍼를 추가하면 output이 바쁠 때 packet을 drop하지 않고 대기시킬 수 있으므로 손실을 줄일 수 있다.
버퍼는 있지만 backpressure가 없는 경우, 모든 output이 busy하고 모든 버퍼가 가득 찼을 때만 packet이 drop된다. Monarch와 유사한 네트워크에 대해 buffering이 있는 경우의 분석은 연습문제 23.9에서 다룬다.

23.5 참고 문헌

• queuing theory의 일반적인 참고 문헌: Kleinrock [99]
• 네트워크에 특화된 모델링 기법: Bertekas [20]
• 네트워크의 probabilistic 분석 예시: Dally [46], Agarwal [2]
• 부분적으로 차 있는 유한 큐에 대한 분석 모델: Dally [47]
• k-ary n-cube 네트워크에서 deadlock에 대한 모델링: Pinkston and Warnakulasuriya [152]

23.6 연습문제

각 문제는 앞서 배운 개념과 분석 기법을 실제 적용해보는 연습이다.

(간략 정리)

• 23.1: 그림 23.10의 트래픽을 비균일하게 수정하여 latency vs. offered traffic 곡선 계산
• 23.2: 4:1 concentrator에서 over-subscription 확률과 average queuing delay 계산
• 23.3: dropping flow control의 queuing 모델 유도
• 23.4: 2-ary 3-fly 회로 스위칭 네트워크의 expected throughput 계산
• 23.5~23.6: k 입력 스위치 및 임의 traffic matrix에 대한 확률적 모델링 확장
• 23.7~23.8: Monarch 네트워크의 duty factor, cost와 loss 간의 관계 그래프화
• 23.9: 버퍼가 추가된 Monarch 네트워크에서 dropping 확률 계산 (F=8인 경우)
• 23.10~23.12: 위 문제들에 대한 simulation 수행 및 모델과의 비교 분석

네트워크 topology는 interconnection network에서 channel과 node의 정적인 배치를 의미한다. 이는 packet이 이동하는 경로에 해당한다. 네트워크 설계의 첫 단계는 topology를 선택하는 것으로, routing 전략과 flow-control 방식이 topology에 크게 의존하기 때문이다. 경로를 선택하고 그 경로를 따라 이동을 계획하기 위해선 먼저 지도(topology)가 필요하다. Chapter 2에서 예시로 보여준 것처럼, topology는 네트워크의 종류(예: butterfly network)뿐 아니라, switch의 radix, stage의 수, 각 channel의 너비와 bit-rate 같은 세부 사항도 정의한다.

좋은 topology를 선택하는 일은 네트워크 요구사항을 사용 가능한 패키징 기술에 맞추는 작업이다. 한편으로는 포트 수, 포트당 bandwidth 및 duty factor가 설계를 이끌고, 다른 한편으로는 칩과 보드당 사용 가능한 핀 수, 배선 밀도, 가능한 signaling rate, 케이블 길이 요구사항이 제약 조건이 된다.

Topology는 비용과 성능에 기반하여 선택된다. 비용은 네트워크를 구현하기 위해 필요한 칩의 수와 복잡도, 이 칩들 간 보드 또는 케이블을 통한 interconnection의 밀도 및 길이에 의해 결정된다. 성능은 bandwidth와 latency 두 요소로 구성되며, 이 둘은 topology 외의 요소들 — 예: flow control, routing 전략, traffic 패턴 — 에 의해서도 영향을 받는다. 따라서 topology만을 평가하기 위해, bisection bandwidth, channel load, path delay 등의 지표를 사용하여 topology가 성능에 미치는 영향을 측정한다.

네트워크 설계자들이 흔히 저지르는 실수 중 하나는, 네트워크의 topology를 당면 문제의 데이터 통신 패턴에 맞추려는 것이다. 표면적으로는 좋은 생각처럼 보인다. 예를 들어, divide-and-conquer 알고리즘을 수행하며 tree-structured communication pattern을 사용하는 머신이라면, tree network가 최적의 선택처럼 보일 수 있다. 하지만 대부분의 경우, 이는 적절하지 않다. 여러 이유로, 특정 목적의 topology는 문제가 발생하기 쉽다. 예를 들어 문제의 동적 부하 불균형이나 문제 크기와 머신 크기 간 불일치로 인해 부하가 잘 분산되지 않을 수 있다. 데이터를 재배치해 부하를 조정하면, 네트워크와 문제 간의 매칭이 무너지게 된다. 또한 특정 문제에 특화된 네트워크는 사용 가능한 패키징 기술과 잘 맞지 않아 긴 배선이나 높은 node degree를 요구하는 경우가 많다. 마지막으로 이런 네트워크는 유연하지 않다. 알고리즘이 바뀌어 다른 통신 패턴을 요구할 경우, 네트워크는 쉽게 변경될 수 없다. 대부분의 경우, 특정 문제에 최적화된 네트워크보다, 일반적인 용도의 좋은 네트워크를 사용하는 것이 훨씬 낫다.

Figure 3.1은 세 가지 예시 topology를 보여준다. (a)는 2차원 torus 구조로 각 차원에 3개의 노드를 가지는 3-ary 2-cube, (b)는 radix-2 butterfly 네트워크로 3-stage 구조인 2-ary 3-fly, (c)는 irregular network다. cube 구조에서는 각 node가 terminal이자 switching node다. 반면 butterfly 구조는 terminal node와 switch node가 구분되며, 가운데에는 switch-only node가 위치한다. 불규칙한 구조도 별도로 제시되어 있다.

3.1 용어 정의

3.1.1 Channels와 Nodes

interconnection network의 topology는 node 집합 N과, 이를 연결하는 channel 집합 C로 정의된다. 메시지는 terminal node 집합 N (단, N ⊆ N)에서 생성되고 종료된다. 모든 node가 terminal인 네트워크에서는 단순히 node 집합을 N으로 표현한다.

각 channel c = (x, y) ∈ C는 source node x와 destination node y를 연결하며, x, y ∈ N이다. channel c의 source는 sc, destination은 dc로 표현한다. Figure 3.1의 각 edge는 양방향 channel 쌍을 의미한다. 이러한 topology 정의는 directed graph와 동일하며, 많은 용어가 graph theory에서 차용되었다. 편의상 node 수는 |N| 대신 N*, channel 수도 |C| 대신 C로 표현한다.

channel c = (x, y)는 다음으로 특징 지어진다:

• 너비 wc 또는 wxy: 병렬 신호의 개수
• 주파수 fc 또는 fxy: 각 신호에서 bit가 전송되는 속도
• 지연 tc 또는 txy: bit가 x에서 y로 도달하는 시간

대부분의 경우, 지연은 물리적 길이 lc와 전파 속도 v의 곱으로 표현된다: lc = vtc. bandwidth는 bc = wc * fc 로 계산된다. 모든 channel의 bandwidth가 동일한 경우, b로 통일해 표현한다.

각 switch node x는 다음과 같은 channel 집합을 가진다:

• 입력 채널 집합: CIx = {c ∈ C | dc = x}
• 출력 채널 집합: COx = {c ∈ C | sc = x}
• 전체 degree: δx = |Cx| = |CIx| + |COx|

모든 node가 같은 degree를 가진다면, δ로 간단히 표현한다.

3.1.2 Direct Network와 Indirect Network

네트워크 node는 packet을 생성하고 소모하는 terminal node, packet을 forwarding하는 switch node, 또는 둘 모두일 수 있다.

• Direct network: 예를 들어 Figure 3.1(a)의 torus에서는 모든 node가 terminal이자 switch이다.
• Indirect network: Figure 3.1(b)의 butterfly에서는 각 node가 terminal(원형) 또는 switch(사각형) 중 하나만 수행한다.

direct network는 terminal node 간에 직접 packet을 전달하고, indirect network는 전용 switch node를 통해 간접적으로 전달한다. Figure 3.1(c)처럼 direct도 indirect도 아닌 network도 존재한다. 모든 direct network는 각 node를 terminal과 switch로 분리하여 indirect 형태로 그릴 수 있다 (Figure 3.2 참조). 이 경우, direct와 indirect 간 구분은 학문적인 의미에 가깝다.

direct network의 장점 중 하나는, terminal의 자원(예: 컴퓨터)을 switch에서도 사용할 수 있다는 점이다. 초기 네트워크에서는 switch 기능이 terminal CPU에서 실행되는 소프트웨어로 구현되었으며, buffer도 terminal의 메모리를 사용했다. 하지만 소프트웨어 switching은 매우 느리고 terminal 자원을 많이 소모하므로, 현재는 거의 사용되지 않는다.

3.1.3 Cuts와 Bisections

 1. Cut (컷)

Cut은 네트워크를 두 부분으로 나누는 것입니다.

• 네트워크의 모든 노드를 두 그룹으로 나눈다고 생각해보세요:
  예를 들어 N1과 N2.
• 그리고 두 그룹(N1과 N2)을 연결하는 channel들을 모읍니다.
• 이 연결선들의 집합을 Cut이라고 부릅니다.

 즉, Cut = 한 쪽에서 다른 쪽으로 가는 channel들의 집합입니다.

 예시

• C와 D 사이에 연결된 선이 있다고 하면, C는 N1에, D는 N2에 있으니 이 선은 Cut에 해당합니다.
• Cut의 개수는 이렇게 두 그룹을 나눴을 때 두 그룹을 연결하는 channel의 수입니다.

2. Bisection (바이섹션)

Bisection은 특별한 종류의 Cut입니다.

• 네트워크의 모든 노드를 거의 반으로 나누는 Cut입니다.
• 그리고 그 반으로 나눈 구역 사이의 channel 수(또는 bandwidth)가 가장 적게 되도록 나눕니다.

즉, Bisection은 네트워크를 거의 반반으로 나누면서, 그 사이를 연결하는 channel 수가 가장 적은 Cut입니다.

왜 중요할까?

• 병목 구간(bottleneck)을 찾을 수 있기 때문입니다.
• 네트워크를 반으로 잘랐을 때, 이 중간 연결(channel) 수가 적으면, 많은 트래픽이 이 작은 연결을 통과해야 하므로 성능이 떨어질 수 있습니다.

3.1.4 Paths

3.1.5 대칭성 (Symmetry)

Topology의 대칭성은 부하 분산과 라우팅에 중요한 역할을 하며, 후속 절들에서 자세히 설명된다. 네트워크가 vertex-symmetric하다는 것은, 임의의 node a를 다른 node b로 mapping하는 automorphism이 존재한다는 뜻이다. 즉, 모든 node의 관점에서 네트워크 구조가 동일하게 보인다는 의미다. 이는 routing을 단순화할 수 있는데, 모든 node가 동일한 네트워크 지도를 공유하므로 동일한 방식으로 목적지로 라우팅할 수 있다.

Edge-symmetric 네트워크는 임의의 channel a를 다른 channel b로 mapping하는 automorphism이 존재한다. Edge symmetry는 모든 channel이 동일하게 취급되므로 channel 간 부하 분산을 개선하는 데 도움이 된다.

🔷 1. Vertex-symmetric (정점 대칭)

"모든 노드가 같은 역할을 하도록 생겼다."

• 네트워크의 어느 노드에서 보더라도 구조가 똑같이 생겼다는 뜻이에요.
• 즉, 한 노드에서 연결된 방향, 수, 거리 등이 다른 노드와 똑같이 생겼다면 vertex-symmetric입니다.
• 쉽게 말해, 노드 입장에서 네트워크가 전부 똑같이 보인다는 뜻이에요.

📌 예:

• 링 (Ring) topology
• Mesh나 Torus도 경우에 따라 vertex-symmetric이 될 수 있어요.

🔷 2. Edge-symmetric (간선 대칭)

"모든 채널이 동일한 역할을 한다."

• **모든 channel (link)**이 구조적으로 같은 위치, 역할을 한다는 뜻이에요.
• 즉, 채널마다 부하가 균등하게 나뉘어질 수 있는 구조라는 의미예요.
• 네트워크 입장에서 어느 channel이든 특별 대우가 없는, "채널 평등"인 셈이에요.

📌 예:

• Torus
• 링
• 어떤 경우엔 vertex-symmetric이 아니어도 edge-symmetric일 수 있어요.

🔷 핵심 차이점 요약

🔷 비유로 쉽게 이해하기

• vertex-symmetric: 모든 사람이 같은 위치, 같은 복장, 같은 키를 가진 군대 → "사람 입장에서 전부 똑같다"
• edge-symmetric: 그 사람들이 가진 총이 전부 똑같고 같은 위치에서 조준함 → "총(채널) 입장에서 전부 똑같다"

3.2 Traffic Patterns

Topology 성능 지표를 도입하기 전에, interconnection network에서 메시지의 공간 분포를 이해하는 것이 유용하다. 이러한 메시지 분포는 traffic matrix λ로 나타내며, λs,d는 node s에서 node d로 전송되는 traffic의 비율을 나타낸다.

Table 3.1은 interconnection network 평가에 사용되는 일반적인 정적 traffic pattern을 나열한다. 이들 중 일부는 실제 애플리케이션에서 나타나는 통신 패턴에 기반하고 있다. 예를 들어, matrix transpose 또는 corner-turn 연산은 transpose pattern을 유도하고, FFT나 sorting 응용은 shuffle pattern, 유체역학 시뮬레이션은 neighbor pattern을 나타낸다.

• Random traffic: source가 모든 destination에 동일 확률로 전송. 가장 일반적으로 사용됨. traffic을 균등하게 분산시켜 부하를 고르게 하므로, load balance가 좋지 않은 topology나 routing 알고리즘도 이 패턴 하에서는 성능이 좋아 보일 수 있다.
• Permutation traffic: 각 source가 하나의 destination에만 전송하며, d = π(s)로 표현된다. traffic matrix λ는 permutation matrix가 되며, 각 행과 열에 단 하나의 값만 존재한다. 특정 source-destination 쌍에 load가 집중되므로, topology와 routing 알고리즘의 부하 분산 능력을 테스트하는 데 적합하다.

Bit permutation은 source 주소의 bit들을 permutation 및 보완하여 destination 주소를 생성하는 방식이다. 예를 들어 source 주소가 {s3, s2, s1, s0}라면:

• bit-reverse: {s0, s1, s2, s3}
• bit-complement: {¬s3, ¬s2, ¬s1, ¬s0}
• shuffle: {s2, s1, s0, s3}

Digit permutation은 radix-k 표현의 digit 단위로 주소를 변형하는 permutation이다. 이 방식은 terminal 주소가 k진수의 n-digit 표현인 경우 (예: k-ary n-cube, k-ary n-fly)에서 사용된다. 예시:

• Tornado pattern: torus topology를 가장 불리하게 만드는 pattern
• Neighbor pattern: locality를 얼마나 잘 활용하는지 측정

3.3 성능 (Performance)

Topology는 비용과 성능을 기준으로 선택된다. 이 절에서는 성능을 결정짓는 세 가지 주요 지표 — throughput, latency, path diversity — 를 설명한다. 3.4절에서는 이 성능 지표들을 네트워크 구현 비용과 연결하여 다시 다룬다.

3.3.1 Throughput과 최대 channel 부하

네트워크가 얼마나 많은 데이터를 처리할 수 있는지, 그리고 가장 부하가 많이 걸리는 채널이 어디인지를 분석하는 내용이다.

Throughput은 네트워크가 input port당 받아들일 수 있는 데이터 속도 (bit/sec)를 말한다. throughput은 routing 및 flow control에 크게 의존하며 topology만으로 결정되지 않는다. 하지만 routing이 부하를 완벽히 분산하고, flow control이 병목 channel에서 idle cycle이 전혀 없다고 가정하면, topology의 이론적 최대 throughput을 계산할 수 있다.

이 절에서는 모든 channel bandwidth가 동일하게 b일 때의 throughput 및 부하 공식만을 다룬다 (Ex.3.5에서는 이 제한을 해제한다).

네트워크의 어떤 channel이 포화(saturated) 상태에 도달할 때가 최대 throughput이다. 포화된 channel이 없다면, 더 많은 traffic을 수용할 수 있으므로 최대 throughput이 아님. 따라서 throughput을 계산하려면 channel load를 고려해야 한다.

channel c의 load γc는, 해당 channel이 감당해야 하는 bandwidth가 input port bandwidth에 비해 얼마나 되는지를 나타내며, 다음과 같이 정의된다. 이는 모든 input이 1 unit의 traffic을 주입할 때 channel c를 통해 지나야 하는 traffic 양으로 해석할 수 있다. 단위가 없고, 일반적으로는 uniform traffic 하에서 계산한다.

​

✅ 핵심 목적

“네트워크가 얼마나 빠르게 데이터를 흘릴 수 있을까?”
→ 이걸 **throughput (처리량)**이라고 하고,
→ **그걸 방해하는 가장 붐비는 통로(channel)**를 bottleneck이라 해요.

🔷 1. Throughput이란?

• Throughput은 각 input port가 초당 얼마나 많은 데이터를 네트워크로 보낼 수 있는지를 의미해요.
• 예를 들어, 모든 노드가 1 Gbit/s로 데이터를 보낸다면, 네트워크는 그 속도를 견뎌야 해요.

🔷 2. 왜 "최대 channel 부하"가 중요할까?

• 네트워크는 여러 channel (통로)로 이루어져 있어요.
• 그런데 일부 channel은 다른 것보다 더 많은 traffic을 받게 돼요.
• 이때 가장 바쁜 channel의 부하를 γmax라고 해요.

📌 이 γmax가 너무 크면 → 그 channel이 병목(bottleneck)이 돼요.
→ 그럼 전체 네트워크 throughput이 그만큼 줄어들어요.

🔷 3. 이상적인 Throughput 계산 공식

책에서 소개하는 공식:

λideal=bγmaxλ_{ideal} = \frac{b}{γ_{max}}λideal​=γmax​b​

• b: 각 channel의 bandwidth (예: 1 Gbit/s)
• γmax: 가장 많이 사용되는 channel의 부하 비율 (무차원값, 단위 없음)

🧠 이 공식이 말하는 것:

"최대 부하 channel이 완전히 포화될 때까지 input에서 데이터를 넣을 수 있다."

🔷 4. 예를 들어 볼게요

• 8-node ring이 있고,
• 각 channel은 1 Gbit/s,
• 모든 노드가 동일하게 데이터를 주고받을 때,
• 가장 많이 사용되는 channel이 1 Gbit/s까지 도달하는 순간이 throughput의 한계예요.

🔷 5. γmax는 어떻게 구하나?

책에서는 몇 가지 방식으로 γmax를 추정하거나 계산하는 방법도 알려줘요:

1. bisection-based 하한:γB=N2BCγ_B = \frac{N}{2BC}γB​=2BCN​(N = 노드 수, BC = channel bisection 수)
2. 전체 채널에 균등 부하 분산하는 상한 공식 (Equation 3.6):γc=1N∑x,y∑P∈Rxy1∣Rxy∣(c가 포함된 경로에 대해서만)γ_{c} = \frac{1}{N} \sum_{x,y} \sum_{P ∈ R_{xy}} \frac{1}{|R_{xy}|} \quad \text{(c가 포함된 경로에 대해서만)}γc​=N1​x,y∑​P∈Rxy​∑​∣Rxy​∣1​(c가 포함된 경로에 대해서만)

✅ 정리하자면

💡 요약 한 줄

3.3.1에서는 "네트워크에서 가장 바쁜 통로가 얼마나 빠르게 꽉 차느냐"를 기준으로 전체 데이터 처리 능력(throughput)을 계산하는 방법을 설명하고 있어요.

3.3.2 지연 (Latency)

이 세 항목은 topology와 물리적 패키징(mapping)에 의해 결정된다:

• Hmin: topology만의 특성
• Dmin: topology 및 패키징 둘 다의 영향을 받음
• b: topology의 node degree와 패키징 제한에 따라 결정

Figure 3.4는 node x에서 z까지 2-hop 경로를 따라 packet이 전달되는 과정을 Gantt 차트로 보여준다:

1. node x에 도착
2. tr 만큼 지연 후 channel x→y로 전송
3. txy 시간 동안 전파
4. y에서 다시 tr 지연 후 y→z로 전송
5. tyz 전파 시간
6. 마지막으로 tail이 도착할 때까지 L/b 시간 직렬화 지연

이 과정을 통해 Equation 3.11의 세 지연 요소가 시각적으로 설명된다.

Figure 3.4의 Gantt 차트에서 latency의 구성 요소가 요약된다. 단일 해치 부분은 routing 지연, 연한 회색 부분은 link latency, 이중 해치 부분은 serialization latency에 해당한다.

예를 들어, 64-node 네트워크에서 평균 hop 수 Havg가 4이고, channel 너비가 16비트인 경우를 생각해 보자. 각 channel c는 1GHz에서 동작하며, 해당 channel을 통과하는 데 tc = 5ns가 걸린다. 단일 router의 지연이 tr = 8ns (2ns clock × 4)일 때, 전체 routing 지연은 8 × 4 = 32ns (16 clocks)이다. wire 지연은 5ns씩 4개로 총 Tw = 20ns (10 clocks)다. packet 길이가 L = 64바이트이고, channel bandwidth가 2GB/s이면 serialization 지연은 64 / 2 = 32ns (16 clocks)이다. 따라서 전체 T₀는 32 + 20 + 32 = 84ns가 된다.

3.3.3 경로 다양성 (Path Diversity)

대부분의 노드 쌍에 대해 minimal path가 여러 개인 네트워크, 즉 |Rxy| > 1인 경우는 |Rxy| = 1인 단일 경로 네트워크보다 더 견고하다. 이러한 path diversity는 채널 간 부하를 분산하고, 고장난 채널이나 노드에도 견딜 수 있도록 하여 네트워크의 신뢰성을 높여준다.

지금까지는 각 노드가 다른 모든 노드로 균등하게 메시지를 보내는 random traffic에 대해 주로 다루었다. 많은 네트워크에서 random traffic은 이상적인 부하이며, 이는 채널 부하를 균등하게 분산시켜주기 때문이다. 그러나 permutation traffic처럼 각 노드가 정확히 하나의 다른 노드로만 메시지를 보낼 때는 상황이 더 까다롭다. 이 경우 path diversity가 부족하면 일부 permutation은 특정 채널에 traffic을 집중시켜 throughput을 심각하게 떨어뜨릴 수 있다.

예를 들어, bit-rotation traffic을 두 가지 topology에서 전송한다고 가정하자:

• 2-ary 4-fly (unit bandwidth)
• 4-ary 2-cube (half-unit bandwidth)

두 네트워크 모두 random traffic에서는 γmax = 1이다. bit-rotation (BR) traffic에서 주소가 {b3, b2, b1, b0}인 노드는 {b2, b1, b0, b3}로 packet을 보낸다. 이는 다음과 같은 shuffle permutation과 같다:

{0, 2, 4, 6, 8, 10, 12, 14, 1, 3, 5, 7, 9, 11, 13, 15}

즉, node 0은 자기 자신에게, node 1은 node 2로, 이런 식이다. Figure 3.5에서처럼, 이 permutation이 2-ary 4-fly에 적용되면 모든 traffic이 네트워크 중앙의 몇 개 채널에 집중된다. 예를 들어:

• node 0, 1, 8, 9 → channel (10, 20)
• node 2, 3, 10, 11 → channel (11, 23)
• node 4, 5, 12, 13 → channel (16, 24)
• node 6, 7, 14, 15 → channel (17, 27)

이 경우 γmax,BR = 4가 되고, throughput은 전체 용량의 25%로 떨어진다.

반면 Figure 3.6에서와 같이, 같은 permutation을 4-ary 2-cube에 적용하면 다음과 같은 결과가 나온다:

• 2개 경로는 채널을 사용하지 않음
• 4개 경로는 채널 1개 사용
• 4개 경로는 채널 2개 사용 (예: H(5,10) = 2, |R5,10| = 2)
• 4개 경로는 채널 3개 사용 (경로 수: 3개)
• 4개 경로는 채널 4개 사용 (경로 수: 24개)

minimal routing만을 사용할 경우, 1-hop 경로가 병목이 된다. 대체 minimal route가 없기 때문이다. 이 경우 γmax,BR = 1이며, uniform traffic에서 γmax = 0.5이므로 throughput은 전체 용량의 50%다.

그러나, 1-hop 경로의 절반을 non-minimal routing으로 우회시키면 부하가 균등해진다. 예를 들어, node 1 → 2 traffic의 절반은 (1,2)로 가고, 나머지 절반은 (1,0)-(0,3)-(3,2) 경로를 사용한다. 이 경우 throughput은 용량의 89%까지 증가하며, 11%의 감소는 non-minimal 경로에서의 hop 수 증가 때문이라 볼 수 있다.

이 예시는 non-minimal routing이 부하 분산에 필수적일 수 있음을 보여준다. 비록 전체적으로 더 많은 경로를 사용하더라도, 네트워크 전체의 성능은 오히려 향상될 수 있다. 그러나 non-minimal routing은 deadlock 방지 등 구현 복잡성을 높이는 단점도 있다 (Chapter 14에서 다룸).

path diversity의 또 다른 중요한 장점은 고장 허용 능력이다. 예를 들어 Figure 3.5의 butterfly network에서 switch 07→17 link가 고장 나면, source 14에서 destination 15로 가는 경로는 존재하지 않는다. 시스템이 커질수록 고장 가능성도 커지므로, 대규모 네트워크는 하나 이상의 노드 또는 link 고장에도 견딜 수 있어야 한다.

한 네트워크의 고장 허용 능력은 edge-disjoint 또는 node-disjoint 경로 수로 측정된다:

• edge-disjoint paths: 공통 link 없이 구성된 경로 집합. 하나의 link 고장이 해당 경로 중 최대 하나에만 영향을 준다.
• 모든 노드 쌍 간 최소 edge-disjoint path 수가 j개라면, j개 미만의 link 고장에는 연결이 보장된다.
• node-disjoint paths: 출발지와 목적지를 제외하고, 공통 노드 없이 구성된 경로 집합. 하나의 노드 고장은 하나의 경로에만 영향을 미친다.
• node-disjoint는 edge-disjoint도 만족하므로, j개 node-disjoint 경로가 있다면 j개 이하의 link 및 node 고장을 견딜 수 있다.

운이 나쁘면, 특정 노드의 이웃 노드, 모든 입력 link, 출력 link가 동시에 고장날 수 있다. 이 경우 해당 노드는 다른 노드로부터 도달도, 전송도 불가능해지며, 이와 같은 고장 수는 다음과 같다:

min⁡x[min⁡{∣CIx∣, ∣COx∣}]\min_x \left[ \min \left\{ |CI_x|,\ |CO_x| \right\} \right]xmin​[min{∣CIx​∣, ∣COx​∣}]

3.4 패키징 비용 (Packaging Cost)

네트워크를 구축할 때, topology의 node들은 물리적 시스템의 packaging 모듈, 칩, 보드, 섀시 등에 매핑된다. topology와 packaging 기술, node 배치는 channel bandwidth 제약을 결정하며, 이 제약 없이는 topology를 평가하거나 비교할 수 없다.

이 절에서는 channel width w가 노드당 핀 수와 전체 global wiring 양에 의해 제한되는 2단계 packaging 계층 모델을 통해 간단한 비용 모델을 정립한다. 또한 bandwidth의 또 다른 구성 요소인 주파수 f가 packaging 선택에 어떻게 영향을 받는지도 다룬다.

첫 번째 계층: router 간 local wiring

• local wiring은 global wiring보다 저렴하고 풍부하므로, topology는 공간적 locality를 활용해 노드 간 거리를 가깝게 유지해야 한다.
• 예: 4×4 배열로 16개의 노드를 하나의 PC 보드에 배치하면, 전체 pin 중 75%가 로컬 연결로 사용 가능하며, 단지 32개 채널만 module 경계를 넘게 된다 (Figure 3.7 참조).

이러한 로컬 배치를 결정한 후, channel width의 주된 제약은 노드당 사용 가능한 핀 수가 된다. 노드당 최대 핀 수를 Wn이라 하면, degree가 δ인 node에서 channel width w는 다음을 만족해야 한다:

w≤Wnδ(3.12)w ≤ \frac{W_n}{δ} \quad (3.12)w≤δWn​​(3.12)

두 번째 계층: global wiring (예: 백플레인)

• 여러 보드를 연결하는 wiring 구조로 구성되며, global signal은 보드 → 커넥터 → 백플레인 → 커넥터 → 다른 보드 순으로 이동한다.
• 이때 사용 가능한 전체 global wires 수 Ws가 각 channel width의 제약이 된다.
• 예: 백플레인을 사용할 경우, 배선 밀도가 제한 요소다.
  • through-hole vias 공간 고려 시, 일반 PC 보드는 신호층당 1 wire/mm 또는 differential signal 기준 0.5 signal/mm 수준
  • 중간 비용 보드는 x, y 방향 각각 4층 → 총 8층 → 방향당 2 signal/mm 가능

Figure 3.7은 4×4 배열의 노드를 하나의 PC 보드에 패키징한 예를 보여준다. 이 구성에서는 전체 노드 핀 중 약 4분의 3이 local wiring으로 연결되어 있다.

bisection은 네트워크를 거의 절반으로 나누면서, 가능한 적은 수의 wire를 절단하는 방식이다. 따라서 bisection으로 나뉜 두 노드 집합은 패키징 시 local group으로 나누기에 좋은 기준이 된다. 이 모델은 일부 네트워크에서는 두 개 이상의 local group으로 나눠야 하는 제약이 있긴 하지만, 대부분의 경우 좋은 근사치를 제공한다.

minimum bisection을 활용하면, 사용 가능한 global wiring에 따라 channel width는 다음 제약을 받는다:

w≤WsBC(3.13)w ≤ \frac{W_s}{BC} \quad (3.13)w≤BCWs​​(3.13)

여기서는 2단계 packaging 계층을 중심으로 설명했지만, 더 큰 시스템에서 필요한 추가 packaging 계층에도 Equation 3.13을 적용할 수 있다.

Equation 3.12와 3.13을 결합하면 channel width에 대한 전체 제약은 다음과 같다:

w≤min⁡(Wnδ, WsBC)(3.14)w ≤ \min \left( \frac{W_n}{δ},\ \frac{W_s}{BC} \right) \quad (3.14)w≤min(δWn​​, BCWs​​)(3.14)

• 첫 번째 항 (Wn/δ)은 degree가 낮은 네트워크 (예: ring)에서 지배적이다. → 이 경우 핀 수 제한형
• 두 번째 항 (Ws/BC)은 degree가 높은 네트워크 (예: binary n-cube)에서 지배적이다. → 이 경우 bisection 제한형

channel width가 아닌 bandwidth 관점에서 제약을 다시 정리할 수도 있다:

• 노드당 최대 bandwidth: Bn=fWnB_n = f W_nBn​=fWn​
• 시스템 bisection 최대 bandwidth: Bs=fWsB_s = f W_sBs​=fWs​

이를 이용하면 channel당 최대 bandwidth b는 다음과 같이 표현된다:

b≤min⁡(Bnδ, BsBC)b ≤ \min \left( \frac{B_n}{δ},\ \frac{B_s}{BC} \right)b≤min(δBn​​, BCBs​​)

패키징 계층에서 고려해야 할 또 다른 중요한 요소는 배선 길이다.

채널 길이는 짧을수록 좋다. 일정 길이 이상이 되면, 신호 주파수가 길이의 제곱에 반비례하여 급격히 감소하기 때문이다:

f=min⁡(f0, f0(lwlc)−2)f = \min \left( f_0,\ f_0 \left( \frac{l_w}{l_c} \right)^{-2} \right)f=min(f0​, f0​(lc​lw​​)−2)

여기서 lc는 주어진 신호율 f₀에서 허용 가능한 감쇠를 기준으로 한 임계 길이(critical length)다.

Table 3.2는 신호율 2GHz에서 다양한 배선 종류에 대한 임계 길이 lc를 나타낸다 (1dB 감쇠 한도 기준):

대부분의 네트워크는 stripguide, fine wire cable 등을 사용한다. 이들은 약 1m 내외의 짧은 거리까지만 지원 가능하며, 이를 넘으면 데이터 속도가 급격히 떨어진다.

Repeater를 삽입하면 긴 채널에서도 고속 동작이 가능하지만, repeater 하나의 비용은 switch 하나와 비슷하다. 따라서 repeater 대신 switch를 삽입하여 channel을 분할하는 것이 더 효율적이다.

즉, 긴 channel이 필요한 topology는 고속 전기식 네트워크에 적합하지 않다.

대안으로 광 신호(optical signaling)를 사용할 수 있다. 광섬유는 전기 배선보다 감쇠와 신호 왜곡이 적어 훨씬 긴 거리(수십~수백 km)를 커버할 수 있다. 단점은 비용이다. 2003년 기준 동일 bandwidth에서 광 채널은 전기 채널보다 10배 이상 비쌌다.

Topology 비교 예시: Figure 3.9는 두 가지 6-node topology의 예를 보여준다.

• (a) 6-node ring: δ = 4, BC = 4
• (b) Cayley graph: δ = 6, BC = 10

패키징 조건:

• Wn = 140핀 / 노드
• Ws = 200 신호 / backplane

패키징 제약을 만족하기 위한 channel width w를 각각 계산:

1. Ring:

w≤min⁡(1404, 2004)=min⁡(35,50)=35(3.15)w ≤ \min \left( \frac{140}{4},\ \frac{200}{4} \right) = \min (35, 50) = 35 \quad (3.15)w≤min(4140​, 4200​)=min(35,50)=35(3.15)

1. Cayley graph:

w≤min⁡(1406, 20010)=min⁡(23.3,20)=20(3.16)w ≤ \min \left( \frac{140}{6},\ \frac{200}{10} \right) = \min (23.3, 20) = 20 \quad (3.16)w≤min(6140​, 10200​)=min(23.3,20)=20(3.16)

신호 주파수 f = 1GHz 기준으로, channel bandwidth는 다음과 같다:

• Ring: 35 Gbit/s
• Cayley graph: 20 Gbit/s

메시지 길이 L = 1024비트, router delay tr = 20ns일 때, 각 topology의 이상적 throughput과 무부하 지연은 Table 3.3에 비교되어 있다.

→ Cayley graph는 higher throughput, Ring은 낮은 지연 시간을 가진다.

왜 이런 결과가 나올까?

• Ring은 pin 수에 의해 channel width가 제한됨 (35)
• Cayley는 bisection 제약으로 제한됨 (20)

따라서:

• Cayley는 bisection 활용이 더 효율적이라 throughput이 높음
• 하지만 channel이 좁아져서 serialization 지연이 커지고, 평균 hop 수 감소 효과를 상쇄함

결론: 단순히 topology만 보면 Cayley가 더 나아 보이지만, 실제 latency는 packaging 제약에 의해 Ring이 더 낮다.

✅ 요약 판단

🔍 NoC에 의미 있는 부분만 요약

1. 채널 수 vs node degree (Wₙ/δ)

• NoC에서도 한 라우터에 몇 개의 입출력 포트를 가질 수 있느냐는 매우 중요한 설계 제약입니다.
• 예: 5-port (N/S/E/W/Local) mesh 라우터 구조 등
• NoC에서는 이것이 cell 면적, 전력, 배선 자원과 직결되므로 Wₙ/δ 제약은 유효합니다.

2. bisection bandwidth

• NoC에서도 mesh, torus, ring 등 다양한 topology의 bisection bandwidth는 network의 bottleneck을 결정합니다.
• 따라서 Chapter 3.4 후반부에서 설명한 "bisection bandwidth가 throughput에 미치는 영향"은 그대로 적용할 수 있습니다.

3. 배선 길이에 따른 주파수 저하 (f ∝ 1/l²)

• chip 내부 배선에서도 long wire delay, insertion buffer, repeater, clock skew, crosstalk 등과 관련된 문제가 있습니다.
• 따라서 완전히 무시할 수는 없지만, NoC 설계자는 H-tree, buffered link 등으로 해결할 수 있습니다.
• → 실제 설계 시 wire pipelining, serialization, 또는 CDN 기술 등을 통해 보완합니다.

✅ 결론

Chapter 3.4 "Packaging Cost"의 전부를 NoC에 적용할 필요는 없지만,
핀 수 제약(Wₙ/δ), bisection bandwidth, 배선 길이와 delay의 관계는
NoC 설계 시에도 반드시 고려할 요소입니다.

3.5 사례 연구: SGI Origin 2000

Figure 3.10은 SGI Origin 서버를 보여준다. 왼쪽은 16-프로세서가 들어간 캐비닛이며, 오른쪽은 8-프로세서 데스크사이드 모델이다.

이 시스템의 네트워크를 살펴보면, interconnection network를 packaging 계층에 매핑하는 데 필요한 여러 문제를 이해할 수 있다. 또한, 소수의 노드에서 수백 개의 노드까지 확장 가능한 시스템을 고정된 구성 요소로 구축할 때 발생하는 이슈들도 알 수 있다.

Origin 2000 네트워크는 SGI의 SPIDER routing chip에 기반한다. 이 칩은 양방향 네트워크 채널 6개를 제공하며, 각 채널은 20비트 폭이고 400 MHz에서 동작한다. 따라서 channel bandwidth는 6.4 Gbit/s가 되고, 하나의 node는 총 6개 채널을 가지므로 노드당 38.4 Gbit/s의 bandwidth를 가진다. 이 모든 채널은 backplane을 통해 구동될 수 있으며, 이 중 3개 채널은 최대 5미터 길이의 케이블을 직접 구동할 수 있다.

Figure 3.11은 Origin 2000 네트워크 topology가 노드 수에 따라 어떻게 변화하는지를 보여준다. 모든 구성에서 각 terminal router는 2개의 processing node(총 4개 프로세서)에 연결된다. 이 terminal 연결은 router의 6개 채널 중 2개를 사용하며, 나머지 4개는 다른 router들과 연결된다.

• 최대 16개 router (32개 노드, 64개 프로세서)로 구성된 시스템은 binary n-cube로 구성되며, 각 router는 최대 4차원 이웃 router에 연결된다 (Figure 3.11(a) 참조).
• 만약 4차원 전체를 사용하지 않는 경우(예: 8-router 시스템), 남은 채널은 머신 전체에 걸쳐 연결되어 네트워크 지름을 줄인다.

주석: 이와 같은 terminal에 여러 processor를 연결하는 방식은 concentration이라 하며, 이는 Section 7.1.1에서 다룬다.

Figure 3.12는 router 수가 16개를 초과하는 시스템에 대해 hierarchical topology를 사용하는 방식을 보여준다.

• 큰 시스템은 8-router (16-node, 32-processor)로 구성된 local subnetwork를 사용하며, 이 subnetwork는 binary 3-cube로 구성된다. 각 node는 채널 하나를 남겨둔다.
• 8개의 router-only global subnetwork가 local subnetwork들 간을 연결한다.
• router가 2ⁿ개인 시스템에서, 각 global network는 m = n − 3 차원의 binary cube로 구성된다.

예시:

• 최대 규모인 256-router (512-node, 1024-processor) 시스템은 32-node binary 5-cube 8개를 global subnetwork로 사용한다.
• local subnetwork j에 있는 router i의 남은 채널은 global subnetwork i의 router j에 연결된다.

특수한 경우:

• 32-node 시스템(n = 5)에서는 각 4포트 global subnetwork가 하나의 router chip으로 구현된다.
• 이 구조는 결과적으로 Clos network 구조이며 (Section 6.3 참조), 각 switch는 binary n-cube로 구성된다.

Figure 3.13은 Origin 2000 시스템의 packaging 구조를 보여준다.

• 각 노드(2프로세서)는 16인치 × 11인치 회로 보드 하나에 패키징된다.
• 각 router chip도 별도의 보드에 패키징된다.
• 노드 보드 4개(= 8프로세서)와 router 보드 2개가 하나의 chassis에 들어가며, 이들은 midplane으로 연결된다.
• chassis 내의 남은 공간은 I/O 서브시스템에 사용된다.
• chassis 2개(= router 4개)가 1개의 캐비닛에 들어간다.
• 시스템은 최대 64개 캐비닛(256 routers)까지 구성될 수 있으며, 대형 시스템의 경우 router 전용 캐비닛이 global subnetwork를 위해 추가된다.

router board의 6개 채널 중:

• 2개: midplane의 노드 보드 2개에 연결
• 1개: midplane 상의 다른 router에 연결
• 3개: back-panel connector를 통해 다른 chassis로 연결됨
  • 1개: 동일 캐비닛 내 다른 chassis에 연결
  • 1개: local subnet 내 두 번째 캐비닛에 연결
  • 1개: global subnetwork 또는 4-cabinet 시스템의 두 번째 캐비닛 쌍에 연결

Table 3.4는 이 hierarchical topology가 shared-memory multiprocessor 시스템의 요구사항을 어떻게 충족하는지를 보여준다. 이 시스템은 모든 router가 6포트라는 제약 하에서 구성된다.

• Equation 3.11에 따라, zero-load latency는 hop 수와 거리(지름)에 비례해 증가한다.
• Equation 3.10의 serialization latency는 채널 너비(20비트)로 고정된다.

Origin 2000은 시스템 크기에 따라 지름(diameter)이 로그 증가하도록 구성된 topology를 사용하여 latency를 낮춘다.

degree-4 binary n-cube 이상의 구조가 필요한 경우, hierarchical network 구조로 확장함으로써 로그 증가 특성을 유지할 수 있다.

또한 이 topology는 shared-memory multiprocessor에 필요한 bandwidth 조건도 만족한다.

• 모든 구성에서 bisection은 총 N개의 채널을 절단한다 (방향당 N/2개, 총 N개).
• 작은 시스템: binary n-cube에서 router 수 2ⁿ개 → bisection을 통과하는 채널 수 = 2ⁿ개 (방향당 2ⁿ⁻¹)
• 큰 시스템: 각 노드는 global subnetwork에 채널 1개를 가지고 있으며, 각 global subnetwork는 그 입력 대역폭만큼의 bisection bandwidth를 가진다.

Table 3.4 Origin 2000 네트워크의 노드 수에 따른 구성 및 성능:

3.6 참고 문헌 노트

이 책의 다음 장에서는 가장 널리 사용되는 두 가지 interconnection network에 중점을 두지만, 주목할 만한 다른 topology들도 존재한다.

• Cube-connected cycles는 hypercube와 동일한 hop 수(diameter)를 유지하면서도 node degree는 고정시킨다【153】.
• Fat tree는 모든 topology를 다항 로그 시간(polylogarithmic time) 안에 모방할 수 있는 보편적(universal) topology로 입증되었다【113】. 예: CM-5 시스템의 네트워크는 4-ary fat tree를 사용【114】.
• Cayley graphs는 cube-connected cycles을 포함하는 topology 집합으로, 간단한 routing과 동일한 크기의 hypercube보다 낮은 degree를 제공한다【7】.

3.7 연습문제

3.1 Tornado traffic in the ring
8-node ring에서 각 노드는 ring을 따라 3 hop 떨어진 노드로 트래픽을 보낸다 (즉, node i는 (i+3 mod 8)로 전송). 각 channel의 bandwidth는 1 Gbit/s이고, 각 input은 512 Mbit/s를 전송한다.

• minimal routing을 사용할 경우 channel load, 이상적 throughput, speedup은?
• non-minimal routing을 허용하고, 거리 기반 확률 분포 (3-hop 경로 5/8, 5-hop 경로 3/8)를 적용했을 때 재계산하라.

3.2 최악의 channel load 하한
최악의 트래픽 조건에서, bisection channel이 가장 높은 부하를 가진다고 가정할 때, 최대 channel load의 하한을 도출하라 (모든 channel의 bandwidth는 b로 동일).

3.3 channel load 상한의 한계
Equation 3.6이 타이트하지 않은 topology를 찾아라. 해당 topology가 부하를 최적으로 분산하기 위해 non-minimal routing이 필요한가? 이유를 설명하라.

3.4 대칭 topology의 channel load 상한의 타당성
edge-symmetric topology에 대해, Equation 3.5 및 3.6의 최대 channel load 상한이 실제 최적 부하와 동일함을 증명하라.

3.5 비대칭 bandwidth에서의 throughput
channel bandwidth가 동일하지 않을 때의 이상적 throughput 식을 도출하라. 필요하다면 γc와 γmax의 정의를 수정하라.

3.6 serialization latency가 topology 선택에 미치는 영향
64개의 processor node를 최소 latency로 연결해야 한다. 각 router는 processor와 동일한 chip에 위치하며 (direct network), processor chip당 네트워크용 pin은 128개다. 각 pin bandwidth는 2 Gbit/s, 평균 packet 길이는 512bit, router의 hop latency는 15ns이다. (wire latency Tw는 0으로 가정)

• (a) fully connected topology의 경우, average router latency Trmin, serialization latency Ts, zero-load latency T₀는?
• (b) ring topology의 경우 (Hmin = 16), latency들을 다시 계산하라.

3.7 non-random 트래픽에서의 latency
Section 1.3.1에서 torus와 ring의 latency는 random traffic 가정 하에 분석되었다. 이 결과로 ring이 더 낮은 latency를 가지는 것으로 나타났다. torus가 더 낮은 latency를 가지는 트래픽 패턴이 존재하는가? 존재하지 않는다면 그 이유는? (torus의 node (i,j)는 ring의 node 4i + j로 매핑된다고 가정)

3.8 Origin 2000에서의 latency
각 Origin 2000 rack은 19인치 너비, 72인치 높이이다. rack 내부 케이블은 48인치, rack 간 케이블은 플로어 아래로 라우팅되며, 케이블의 전파 속도는 2×10⁸ m/s이다. 메시지는 512비트 길이(32비트 word 16개).

• node 수가 16개 및 512개인 Origin 2000에 대해 wire delay Tw를 포함한 평균 zero-load latency를 계산하라 (uniform traffic 가정).

3.9 partially random wiring의 diameter 개선
random topology는 low diameter 등 좋은 특성을 가지나, 포장 및 routing 정규성 측면에서 비실용적일 수 있다.
Figure 3.14(a)의 mesh 네트워크에서, 좌우는 서로 다른 cabinet에 포장되어 있고, coaxial cable로 대응 node가 연결되어 있다.

• (a) 이 mesh network의 diameter는?
• (b) 케이블 연결을 무작위로 섞으면 diameter는 어떻게 변화하는가? (Figure 3.14(b) 참조). 모든 permutation 중 최소/최대 diameter는? 최소 diameter를 실현하는 permutation은?

3.10 fat tree 네트워크 성능
Figure 3.15는 16-node, radix-2 fat tree를 보여준다.

• (a) 모든 channel bandwidth가 terminal node의 injection/ejection rate와 같다면, 네트워크의 capacity는?
• (b) 다음과 같은 random routing을 사용할 경우: 패킷은 source에서 “위쪽”으로 올라가면서 두 개의 up 채널 중 임의 선택, 이후 “아래쪽” 경로로 destination까지 라우팅. 어떤 트래픽 패턴에서든 최대 channel load는 얼마까지 가능한가?

3.11 cube-connected cycles topology의 성능과 패키징
Figure 3.16은 3차 order cube-connected cycles이다.

• (a) channel bisection BC는?
• (b) minimal routing을 사용할 경우, 최대 hop 수 Hmax와 평균 hop 수 Hmin은?
• (c) 다음 제약 하에 이 topology를 패키징하라: Wn = 128 signals/node, Ws = 180 signals/backplane. packet 길이 L = 200bit, 주파수 f = 800 MHz, wire 길이는 무시. channel width w의 최대값은? pin 제한인가 bisection 제한인가? zero-load latency를 75ns로 맞추기 위한 router latency tr 값은?

3.12 성능의 물리적 한계
단순한 가정을 통해, 패키징된 네트워크의 diameter와 노드 간 거리의 실현 가능한 하한을 계산할 수 있다.

• (a) radix k switch를 사용할 경우, N-node 네트워크의 최소 diameter는?
• (b) 노드가 부피 V를 가질 때, 3차원에서 노드 간 최대 거리를 최소화하는 packaging 형태는? 많은 수의 노드를 가정할 때 이 거리는 얼마인가?

이 장에서는 간단한 interconnection network의 구조와 설계를 살펴보며 전체적인 개요를 제공한다. 가장 단순한 형태의 네트워크인 butterfly network with dropping flow control을 다룬다. 이 네트워크는 비용이 많이 들지만, interconnection network 설계의 주요 개념을 강조하는 데 유용하다. 이후 장에서는 더 효율적이고 실용적인 네트워크를 만드는 방법을 다룰 것이다.

2.1 Network Specifications and Constraints

모든 공학적 설계 문제와 마찬가지로, 네트워크 설계는 무엇을 만들고 싶은지를 정의하는 사양(specifications)과 가능한 해법의 범위를 제한하는 제약조건(constraints)에서 출발한다. 이 장에서의 예제 네트워크 사양은 아래의 Table 2.1에 요약되어 있다. 네트워크의 크기(64개의 포트)와 포트당 요구되는 bandwidth가 포함된다. 테이블에서 보이듯, peak bandwidth와 average bandwidth가 같으며, 이는 입력이 0.25 Gbyte/s의 속도로 지속적으로 메시지를 inject한다는 것을 의미한다. 각 입력이 각 출력을 동일한 확률로 선택하는 random traffic이 예상되며, 메시지 크기는 4~64 bytes이다. 또한 QoS와 신뢰성 사양은 packet drop을 허용한다. 즉, 모든 packet이 목적지에 반드시 전달될 필요는 없다. 이는 flow control 구현을 단순하게 만들어준다. 실제 시스템에서는 dropped packet의 비율과 조건 등을 명시한 더 상세한 QoS 사양이 포함되겠지만, 여기서는 설계 개념을 설명하는 데 이 정도면 충분하다.

예제 네트워크 설계의 제약조건은 Table 2.2에 정리되어 있다. 이 제약은 각 수준의 패키징(capacity and cost)을 정의한다. 네트워크는 chip들로 구성되고, chip은 circuit board에 실장되며, board는 cable로 연결된다. 제약조건은 각 계층에서 module interface를 통해 전송할 수 있는 signal 수와 각 module의 비용을 지정한다. cable의 경우, bandwidth 감소 없이 도달할 수 있는 최대 거리도 명시되어 있다.

1. signal은 반드시 pin을 의미하지는 않는다. 예를 들어, differential signaling에서는 signal당 두 개의 핀이 필요하다.
2. bandwidth × distance² (Bd²)가 일정한 케이블의 특성상, 2배 길이로 전송할 경우 bandwidth는 4분의 1로 줄어든다.

Table 2.1 Example Network Specifications

Table 2.2 Example Network Constraints

2.2 Topology

예제 네트워크는 단순화를 위하여 butterfly topology를 갖는다. 하나의 입력 포트 입장에서 보면, butterfly는 tree처럼 보인다(Figure 2.1 참고). 각 단계(level)는 switching node로 구성되며, 이들은 terminal node와 달리 packet을 보내거나 받지 않고 전달만 한다. 또한 channel은 unidirectional로, 화살표 방향(입력에서 출력, 왼쪽에서 오른쪽)으로 흐른다. topology로 butterfly를 선택했지만, 이는 아직 설계의 절반이다. network의 speedup, butterfly의 radix, 그리고 topology의 패키징 맵핑을 결정해야 한다.

speedup은 network의 총 입력 bandwidth와 이상적인 network capacity의 비율이다. 여기서 capacity는 이상적인 라우팅과 flow control이 있다고 가정했을 때 가능한 최대 throughput이다. speedup이 1이면, 입력 요구량과 네트워크가 제공할 수 있는 용량이 일치한다는 의미이다. 더 큰 speedup을 제공하면 여유(margin)가 생기며 비이상적 상황에 대응할 수 있다. 이는 건축의 안전계수(safety factor) 개념과 유사하다.

butterfly에서 각 channel의 bandwidth를 입력 포트와 동일하게 설계하면 speedup은 1이 된다. random traffic에서는 각 입력이 모든 출력에 균등하게 보내기 때문에, 모든 channel은 동일한 수요를 받는다. 본 예제에서는 각 channel이 0.25 Gbyte/s의 bandwidth를 갖는다. 하지만, 단순성을 위해 speedup 8을 선택한다. 이는 매우 큰 수치지만(브루클린 브리지는 safety factor 6), 이후에는 이 수치를 줄이는 법을 배운다.

speedup과 패키징 제약조건을 고려하여, 각 switch node의 입력/출력 수(radix)가 결정된다. 예를 들어, Figure 2.1의 butterfly는 radix 2이다. 하나의 switch node는 chip 하나에 구현되며, chip당 총 signal 수는 150을 넘지 않아야 한다. speedup 8을 구현하려면 8 × 0.25 = 2 Gbyte/s의 channel bandwidth가 필요하고, 이는 1 Gbit/s의 signal 16개를 사용하여 구성된다. 여기에 overhead signal 2개를 더하면, channel은 18 signal로 구성되며, chip당 150/18 ≈ 8개의 channel만 탑재 가능하다. 따라서 radix-4 butterfly, 즉 입력/출력 4개씩을 가지는 switch node를 선택한다.

64개의 출력 포트에 연결하려면 log₄64 = 3 단계의 switch node가 필요하다. 따라서 이 네트워크는 radix-4, 3-stage butterfly, 즉 4-ary 3-fly이다. 전체 topology는 Figure 2.2에 나와 있다. Figure 2.1의 확장판이며, input 1에서 시작해 64개의 출력으로 향하는 경로는 여전히 tree 형태이며, tree의 degree는 radix인 4이다.

topology 설계의 마지막 단계는 패키징이다. 이미 각 switch node를 chip 하나로 배치하기로 결정했다. radix를 chip 제약조건에 맞춰 정했기 때문에, chip은 설계 제약을 충족한다. 이제 이 chip을 board에 실장해야 하며, 비용을 최소화하기 위해 한 board에 가능한 많은 chip을 넣고 싶다. 하지만 board당 signal 수는 750을 초과할 수 없다. 이는 커넥터 한쪽 면을 통해 보낼 수 있는 최대 signal 수, 즉 connector density × 길이에 의해 결정된다.

유효한 board 간 partitioning은 Figure 2.2에 표시되어 있으며, 각 board의 경계는 점선 상자로 나타나 있다. 첫 번째 stage는 4개의 board에, board당 4개의 chip으로 배치된다. 다음 두 stage는 4개의 board에, board당 8개의 chip으로 배치된다. 각 board에는 18 signal로 구성된 channel이 32개 입출력되며, 총 32 × 18 = 576 signals로 제약을 만족한다.

각 board에는 총 32개의 channel이 존재하며, 각 channel은 18개의 signal을 사용하므로 총 576 signal이 필요하다. 이는 750 signal 제한 내에 충분히 들어간다. 날카로운 독자는 첫 번째 stage의 board에 router chip 5개를 실을 수도 있다고 생각할 수 있다(40개 channel, 즉 720 signals). 하지만 그렇게 하더라도 여전히 4개의 첫 번째 stage board가 필요하므로 비효율적이다. 또한 두 번째 stage의 board에 router chip 10개를 실을 수는 없다. 필요한 46개 채널은 총 828 signal이 되며, board의 pinout을 초과하기 때문이다.

마지막으로, board 간 연결은 Figure 2.3에서 보듯이 cable을 통해 이루어진다. 그림의 굵은 회색 선 하나는 하나의 cable을 나타내며, 이는 하나의 circuit board에서 다른 board로 18-bit channel 4개를 전달한다. 8개의 circuit board는 이런 cable 16개로 연결된다. 즉, 각 첫 번째 stage board에서 두 번째 및 세 번째 stage board로 각각 cable을 연결한다. 이 8개의 board가 하나의 chassis 내에 배치되므로 cable의 길이는 제약 내에 있다.

한 걸음 물러서서 보면, 이 topology에서 어떻게 모든 입력을 모든 출력에 연결할 수 있는지 확인할 수 있다. 첫 번째 stage의 switch는 나머지 stage가 있는 4개의 circuit board 중 하나를 선택한다. 두 번째 stage는 선택된 board 내의 4개의 chip 중 하나를 선택한다. 마지막 stage는 원하는 출력 포트를 선택한다. 이러한 분할 정복(divide-and-conquer) 구조는 패킷을 라우팅할 때 효율적으로 사용된다.

2.3 Routing

우리의 단순한 butterfly network는 destination-tag routing을 사용한다. 이는 destination address의 비트를 이용해 네트워크의 각 단계에서 출력 포트를 선택하는 방식이다.

64개의 노드를 갖는 이 네트워크에서 destination address는 6비트이다. 각 switch는 이 중 2비트(dibit)를 사용하여 4개의 출력 중 하나를 선택하고, 이는 남은 노드 집합의 1/4로 라우팅된다.

예를 들어, 입력 포트 12에서 출력 노드 35 (= 100011₂)로 패킷을 보내는 경우를 보자. 가장 상위 dibit인 10은 switch 0.3의 세 번째 출력 포트를 선택하여 패킷을 switch 1.11로 보낸다. 그 다음 중간 dibit 00은 switch 1.11의 첫 번째 출력 포트를 선택하여 패킷을 switch 2.8로 보낸다. 마지막으로 가장 하위 dibit 11은 switch 2.8의 마지막 출력 포트를 선택하여 출력 포트 35로 패킷을 전달한다.

이러한 출력 포트 선택 순서는 입력 포트와 무관하다. 예를 들어, 입력 포트 51에서 출력 포트 35로 보내도 같은 선택 순서를 따른다. 즉, 라우팅 알고리즘은 패킷과 함께 destination address만 저장하면 된다.

일관성을 위해, 모든 switch node는 destination address의 가장 상위 dibit만 참조한다. 그런 다음, 패킷이 node를 떠나기 전에 address는 왼쪽으로 2비트 shift되어 방금 사용한 bit는 제거되고 다음 dibit이 상위 위치로 올라온다. 예를 들어, node 35로 라우팅을 시작할 때 address 100011₂는 shift 되어 001100₂이 된다.

이러한 convention 덕분에 모든 switch node가 동일한 방식으로 동작할 수 있고, 특별한 설정 없이도 사용 가능하다. 또한, address field의 크기만 확장하면 더 많은 노드를 가지는 네트워크로 확장할 수 있다.

2.4 Flow Control

이 네트워크의 각 채널은 한 cycle당 16-bit의 physical digit, 즉 phit을 전달한다. 그러나 네트워크는 32~512bit 크기의 전체 패킷을 전달해야 하므로, Figure 2.4에 제시된 간단한 프로토콜을 사용하여 여러 phit을 packet으로 조립한다.

각 packet은 header phit으로 시작하고, 그 뒤에 0개 이상의 payload phit가 따라온다. header phit은 새로운 packet의 시작을 나타내며, 라우팅 알고리즘에 사용될 destination address도 포함한다. payload phit은 실제 데이터를 담고 있으며, 16-bit 단위로 나뉜다.

하나의 packet을 구성하는 phit은 연속적이어야 하며, 중간에 끊기지 않아야 한다. 단, packet 사이에는 얼마든지 null phit이 있을 수 있다. 각 16-bit word가 header인지 payload인지 또는 null인지 구별하기 위해, 각 채널에 2-bit type field를 추가로 붙인다.

이 field는 다음과 같은 역할을 한다:

• H: Header
• P: Payload
• N: Null

따라서 각 packet은 하나의 H word와 그 뒤를 따르는 0개 이상의 P word, 그리고 0개 이상의 N word로 구성된다. 이를 정규 표현식으로 표현하면 (HP*N*)* 형식이다. 즉, link 위에는 여러 개의 packet이 흐를 수 있으며, 각 packet은 위의 구조를 갖는다.

이제 phit을 packet으로 조립했으니, flow control의 핵심, 즉 packet에 자원을 할당하는 과정으로 넘어간다. 단순화를 위해, 우리의 butterfly network는 dropping flow control을 사용한다. 패킷이 switch에 도달했을 때 필요한 output port가 사용 중이면, 해당 packet은 drop (폐기)된다. 이러한 flow control은 end-to-end error control protocol이 존재함을 가정하고 있다.

Figure 2.4는 네트워크에서 사용되는 packet format을 보여준다. 세로 방향은 시간(cycle)을, 가로 방향은 채널의 18개 signal을 나타낸다. 왼쪽 2개 signal은 phit type (H, P, N)을 담고, 나머지 16개 signal은 destination address 또는 data를 담거나 null일 경우 비워진다.

Table 2.3은 이 네트워크에서 사용하는 phit type의 encoding을 보여준다:

패킷을 재전송하는 역할은 상위의 end-to-end error control protocol이 담당할 것으로 가정한다. 패킷을 drop하는 것은 가장 비효율적인 flow control 방식 중 하나이다. 패킷 손실률이 높고, 결국 drop되는 패킷에 채널 bandwidth를 낭비하게 된다. 이보다 훨씬 나은 flow control 기법들이 있으며, Chapter 12에서 다룬다. 그러나 이 장에서는 개념과 구현이 매우 단순하기 때문에 dropping flow control이 적합하다.

2.5 Router Design

butterfly network의 각 switching node는 router로, 입력으로부터 패킷을 받고, 라우팅 알고리즘에 따라 목적지를 결정한 후, 적절한 출력으로 패킷을 전달한다. 지금까지의 설계 결정은 매우 단순한 router를 가능하게 한다.

Figure 2.5는 router의 block diagram이다. 이 router의 datapath는 다음으로 구성된다:

• 18-bit input register 4개
• 18-bit 4:1 multiplexer 4개
• routing field를 shift하는 shifter 4개
• 18-bit output register 4개

총 144-bit의 register와 약 650개의 2-input NAND gate에 해당하는 회로가 사용된다.

phit은 매 cycle마다 input register에 도착하며, 모든 multiplexer로 전달된다. 각 multiplexer에서 연결된 allocator는 각 phit의 type과 header phit의 next hop field를 검사하고 switch를 설정한다.

선택된 입력의 phit은 이후 shifter로 전달된다. allocator의 제어 하에, header phit은 routing field를 왼쪽으로 2비트 shift하여 현재 field를 제거하고 다음 field를 노출한다. payload phit은 변경 없이 그대로 전달된다.

router의 제어는 전적으로 4개의 allocator에 의해 이루어진다. 이들은 각 출력 포트를 제어하며 multiplexer와 shifter를 조작한다. allocator는 4개의 입력 중 하나에 출력 포트를 할당한다.

Allocator 구성 (Figure 2.6)

각 allocator는 거의 동일한 구조의 bit slice 4개로 구성되며, 각 slice는 다음 세 영역으로 나뉜다:

1. Decode
   • 각 입력 phit의 상위 4비트를 해독한다.
   • request_i: 입력 i의 phit이 header이고, route field의 상위 2비트가 현재 출력 포트 번호와 일치하면 true
   • payload_i: 입력 i의 phit이 payload이면 true
2. Arbitrate
   • 4-input fixed-priority arbiter를 사용한다.
   • 요청 신호 중 첫 번째(위쪽부터)의 입력에 grant를 부여한다.
   • grant 시, 해당 입력을 multiplexer에서 선택하도록 select 신호를 활성화
   • header가 통과하면 shift 신호도 활성화되어 routing field를 shift함
3. Hold
   • 동일한 packet의 payload가 따라오는 동안, 출력을 해당 입력에 고정
   • last_i는 이전 cycle에 선택된 입력을 기억
   • 이번 cycle에도 payload가 입력되면, hold_i를 활성화하고 avail을 비활성화하여 새로운 header의 할당을 막는다

Note: 실제 시스템에서는 fixed-priority arbiter는 사용하지 않는다. 불공정성과 livelock 또는 starvation 문제를 유발하기 때문이다. Chapter 18과 19에서 더 나은 arbitration 방법들을 다룬다.

Verilog RTL 모델 (Figure 2.7)

아래는 Figure 2.6의 allocator를 Verilog로 구현한 것이다.

• 각 입력 phit에서 routing 정보와 type 정보를 해석
• 현재 출력 포트(thisPort)에 맞는 입력을 선택
• payload가 이어질 경우 hold 상태 유지
• shift 제어 신호를 통해 header field를 업데이트
• 고정 우선순위 방식으로 grant 결정

Verilog는 텍스트 기반으로 하드웨어를 기술할 수 있는 편리한 방법이며, simulation 및 synthesis input 언어로도 사용 가능하다. 따라서 이 방식으로 기술한 후 simulation으로 동작을 검증하고, ASIC 또는 FPGA를 위한 gate-level 디자인으로 synthesis할 수 있다.

// simple four-input four output router with dropping flow control
module simple_router(clk,i0,i1,i2,i3,o0,o1,o2,o3) ;

input clk ; // chip clock
input [17:0] i0,i1,i2,i3 ; // input phits
output [17:0] o0,o1,o2,o3 ; // output phits

reg [17:0] r0,r1,r2,r3 ; // outputs of input registers
reg [17:0] o0,o1,o2,o3 ; // output registers
wire [17:0] s0,s1,s2,s3 ; // output of shifters
wire [17:0] m0,m1,m2,m3 ; // output of multiplexers
wire [3:0] sel0, sel1, sel2, sel3 ; // multiplexer control
wire shift0, shift1, shift2, shift3 ; // shifter control

// the four allocators
alloc a0(clk, 2’b00, r0[17:14], r1[17:14], r2[17:14], r3[17:14], sel0, shift0) ;
alloc a1(clk, 2’b01, r0[17:14], r1[17:14], r2[17:14], r3[17:14], sel1, shift1) ;
alloc a2(clk, 2’b10, r0[17:14], r1[17:14], r2[17:14], r3[17:14], sel2, shift2) ;
alloc a3(clk, 2’b11, r0[17:14], r1[17:14], r2[17:14], r3[17:14], sel3, shift3) ;

// multiplexers
mux4_18 mx0(sel0, r0, r1, r2, r3, m0) ;
mux4_18 mx1(sel1, r0, r1, r2, r3, m1) ;
mux4_18 mx2(sel2, r0, r1, r2, r3, m2) ;
mux4_18 mx3(sel3, r0, r1, r2, r3, m3) ;

// shifters
shiftp sh0(shift0, m0, s0) ;
shiftp sh1(shift1, m1, s1) ;
shiftp sh2(shift2, m2, s2) ;
shiftp sh3(shift3, m3, s3) ;

// flip flops
always @(posedge clk)
begin
r0=i0 ; r1=i1 ; r2=i2 ; r3=i3 ;
o0=s0 ; o1=s1 ; o2=s2 ; o3=s3 ;
end
endmodule

2.6 Performance Analysis

dropping flow control에서는 성능 지표들이 패킷이 drop될 확률에 크게 영향을 받는다.

네트워크 모델 (Figure 2.9)

Dropped packet을 재전송한다고 가정하고, 간단한 모델로 분석을 시작한다.
입력과 출력 사이의 대칭성, random traffic 패턴 때문에, 하나의 입력만 고려하면 충분하다.

• 패킷은 λ의 비율로 네트워크에 주입된다.
• λ는 2 Gbyte/s 채널 대역폭으로 정규화되어 있으며, λ = 1은 최대 속도 의미.
• 재전송되는 패킷도 합쳐져서 p₀라는 총 주입률이 된다.

각 단계에서:

• 일부 패킷은 충돌로 drop됨.
• 다음 단계로 통과하는 비율은 p₁, p₂, p₃.
• drop된 패킷은 입력으로 다시 돌아가며 재전송됨.

수식 (Equation 2.2)
네트워크의 각 stage i에서 다음 stage의 출력률 pᵢ₊₁은 다음과 같다:

pi+1=1−(1−pi4)4p_{i+1} = 1 - \left(1 - \frac{p_i}{4} \right)^4pi+1​=1−(1−4pi​​)4

입력 λ = 0.125 (speedup = 8)일 때, 각 stage 출력은:

• p₁ = 0.119
• p₂ = 0.114
• p₃ = 0.109

즉, 입력이 0.125일 때 실제 throughput은 0.109이며, 0.016(=12.6%)는 drop된다.

재전송의 피드백

drop된 패킷의 재전송은 전체 입력률 p₀를 증가시키고, 이는 또 drop률을 높인다. 이 과정이 안정되면, 다음 조건이 성립한다:

• 안정 조건: p₀ ≤ 1
• 최종적으로 p₃ = λ 이면 수렴

Throughput 곡선 (Figure 2.10)

Figure 2.10은 injection rate에 따른 throughput을 보여준다.

• 낮은 부하: throughput ≈ injection rate
• 높은 부하: drop이 심해져 throughput 감소
• 포화(saturation): 최대 throughput은 0.432 (43.2%)
• 재전송을 하든 안 하든, 이 이상은 낼 수 없다.

따라서 이 네트워크는 speedup 2.5 이상이면 충분하지만, latency 개선을 위해 speedup 8을 선택한 것이다.

dropping flow control이 실제 사용되지 않는 이유는 바로 이 throughput의 비효율성 때문이다.
Chapter 12에서는 채널 대역폭의 90% 이상을 효율적으로 사용하는 flow control 기법들을 소개한다.

Latency 모델

latency도 channel capacity 기준으로 정규화한다.
패킷이 drop 없이 네트워크를 통과할 때는 6-cycle의 지연이 있다. 이를 relative latency = 1.0으로 정의.

하지만 drop되는 패킷은 다시 전송되며, latency가 누적된다.

• drop 비율 pᴰ:PD=p0−p3p0P_D = \frac{p_0 - p_3}{p_0}PD​=p0​p0​−p3​​
• 평균 latency T는 다음 수식으로 계산:

T=∑i=0∞(i+1)PDi(1−PD)=11−PD=p0p3T = \sum_{i=0}^\infty (i+1) P_D^i (1 - P_D) = \frac{1}{1 - P_D} = \frac{p_0}{p_3}T=i=0∑∞​(i+1)PDi​(1−PD​)=1−PD​1​=p3​p0​​

(Figure 2.11에 그래프 있음)

• throughput이 0.39일 때 latency는 2배가 된다.
• throughput이 0.43에서 포화, 그 이상은 latency 증가만 발생

실제 시스템에서는 drop을 즉시 감지하고 6 cycle 내에 재전송하는 것은 비현실적이다.
재전송 패킷과 신규 패킷이 충돌할 가능성이 증가하므로, queueing delay도 고려해야 한다.
Figure 2.11은 queueing이 포함된 latency 곡선도 함께 보여준다. 이 곡선은 포화에 가까워질수록 무한대로 증가하는 전형적인 interconnection network의 형태를 갖는다.

Figure 2.11은 offered traffic (injection rate)에 따른 relative latency를 나타낸다.
실선은 본문에서 제시한 단순 모델을, 점선은 queueing delay를 고려한 모델을 나타낸다.

Equation 2.3과 Figure 2.11은 평균 latency만을 보여준다.
하지만 많은 응용에서는 평균뿐만 아니라 latency의 분포, 특히 최악의 latency나 **latency의 변동성(jitter)**이 중요하다.
예를 들어, 비디오 재생 시스템에서는 패킷을 재생 전에 저장하는 버퍼 크기는 평균 latency가 아니라 jitter에 의해 결정된다.

우리 예제 네트워크에서는, relative latency가 정확히 i가 될 확률은 다음과 같다:

P(T=i)=PDi−1(1−PD)P(T = i) = P_D^{i - 1} (1 - P_D)P(T=i)=PDi−1​(1−PD​)

이러한 지수 분포는 이론상 무한한 최대 latency와 무한한 jitter를 의미한다.
현실적으로는 전체 패킷 중 일정 비율(예: 99%)이 도달하는 데 걸리는 최대 지연 시간으로 jitter를 정의할 수 있다.

지금까지 논의된 성능 측정은 모두 uniform random traffic을 기준으로 한다.
butterfly network에서는 이것이 최상의 경우이다.
그러나, 예를 들어 bit-reversal과 같은 특정 traffic pattern에서는 성능이 훨씬 나빠질 수 있다.

bit-reversal traffic pattern:
이진 주소 {bₙ₋₁, bₙ₋₂, ..., b₀}를 가진 노드가 {b₀, b₁, ..., bₙ₋₁}를 목적지로 패킷을 보낸다.

이처럼 성능이 나빠지는 주요 원인은 각 입력에서 출력까지 경로가 단 하나이기 때문이다.
경로 다양성(path diversity)이 있는 네트워크는 이러한 부하 조건에서도 훨씬 좋은 성능을 보인다.

2.7 Exercises

2.1 Simple Network의 비용
Table 2.1과 2.2의 데이터를 이용하여 이 단순 네트워크의 비용을 계산하라.

2.2 전력 제한 조건 추가
board당 chip 개수를 6개로 제한하자. 이는 chip에 충분한 전력을 공급하고 열을 적절히 분산시키기 위함이다.
이 새로운 제약 조건을 포함하면서 기존 조건도 만족하는 packaging을 설계하라. 해당 packaging의 비용은?

2.3 공정한 allocator
Figure 2.7에 제시된 Verilog allocator 코드를 수정하여 더 공정한 arbitration을 구현하라.
시뮬레이션을 통해 새 allocator를 검증하고 설계를 설명하라.

2.4 router의 degree 확장
simple router를 4×4가 아닌 5×5 switch로 확장한다면, 이를 2-D mesh 또는 torus network 구현에 사용할 수 있다.
router와 packet format을 어떻게 확장해야 할지 설명하라.

2.5 재전송 우선 처리
Verilog 코드를 수정하여 재전송 패킷에 우선권을 부여하라.
예를 들어, 동일한 switch에서 두 개의 head phit이 동일한 출력을 요청할 경우,
항상 재전송된 패킷이 우선권을 갖도록 한다.
이를 위해 phit header에 priority field를 추가하고, 패킷이 재주입될 때 이 필드가 적절히 설정된다고 가정한다.

2.6 여러 번 drop되는 것 줄이기
2.5에서 제안한 것처럼 동일한 패킷이 여러 번 drop되는 것을 줄이면,
평균 latency는 감소하는가? 그 이유를 설명하라.

2.7 butterfly 확장에 따른 drop률 변화
예제 butterfly network에 stage를 추가하여 노드 수를 늘리면, drop되는 패킷의 비율은 어떻게 될까?
반대로, switch의 degree를 증가시키면 어떻게 될까?
drop 확률만을 고려할 때, 노드를 늘릴 경우 stage를 늘리는 것과 switch degree를 키우는 것 중 무엇이 더 효율적인가?

2.8 현실적인 drop delay
실제 네트워크에서는 drop된 패킷을 다시 전송하기까지 상당한 지연이 존재한다.
예를 들어, acknowledgment가 source에 도달하고, timeout까지 기다려야 한다.
이러한 delay를 반영하여 Equation 2.3을 수정하라.

2.9 시뮬레이션
우리 예제 네트워크를 시뮬레이션하는 간단한 프로그램을 작성하라.
이를 통해 injection rate에 따른 latency를 실험적으로 측정하라.
결과를 Equation 2.3과 Figure 2.11의 분석 결과, 그리고 queueing 모델과 비교하라:

T=T02+p0p3(T02+p02(1−p0))T = \frac{T_0}{2} + \frac{p_0}{p_3} \left( \frac{T_0}{2} + \frac{p_0}{2(1 - p_0)} \right)T=2T0​​+p3​p0​​(2T0​​+2(1−p0​)p0​​)

여기서 T0T_0T0​는 zero-load latency, 즉 drop되지 않은 패킷의 latency이다.

2.10 timeout 메커니즘 추가
Exercise 2.9의 시뮬레이터에 timeout 기능을 추가하라.
Exercise 2.8에서 제시된 모델과 비교하고, 주요 차이점을 설명하라.

디지털 시스템은 현대 사회에 만연해 있다. 디지털 컴퓨터는 물리 시스템의 시뮬레이션, 대규모 데이터베이스 관리, 문서 작성 등 다양한 작업에 사용된다. 디지털 통신 시스템은 전화 통화, 비디오 신호, 인터넷 데이터를 전달한다. 오디오와 비디오 엔터테인먼트 역시 점점 디지털 형태로 전달되고 처리된다. 마지막으로, 자동차부터 가전제품까지 거의 모든 제품이 디지털 방식으로 제어된다.

디지털 시스템은 세 가지 기본 구성 요소로 이루어진다: logic, memory, communication.

• Logic은 데이터를 변형하거나 조합한다. 예를 들어 산술 연산을 하거나 결정을 내리는 기능이다.
• Memory는 데이터를 나중에 사용할 수 있도록 저장하며, 시간적으로 이동시킨다.
• Communication은 데이터를 한 위치에서 다른 위치로 이동시킨다.

이 책은 디지털 시스템의 communication 구성 요소를 다룬다. 특히, 디지털 시스템의 서브시스템 간 데이터 전송에 사용되는 interconnection network를 다룬다.

오늘날 대부분의 디지털 시스템에서 성능의 병목은 logic이나 memory가 아니라 communication 또는 interconnection에서 발생한다. 고급 시스템에서는 전력의 대부분이 배선을 구동하는 데 사용되며, 클럭 주기의 대부분은 gate delay가 아니라 wire delay에 소모된다. 기술이 발전함에 따라 메모리와 프로세서는 더 작고, 빠르고, 저렴해지지만 빛의 속도는 변하지 않는다. 시스템 구성 요소 간 interconnection을 결정짓는 핀 밀도와 배선 밀도는 구성 요소 자체보다 느리게 스케일링되고 있다. 또한 구성 요소 간 통신 빈도는 최신 프로세서의 클럭 속도에 비해 현저히 뒤처지고 있다. 이러한 요인이 결합되어 interconnection은 향후 디지털 시스템의 성공을 좌우하는 핵심 요소가 되었다.

설계자들이 제한된 interconnection bandwidth를 보다 효율적으로 활용하려고 노력하면서, interconnection network는 현대 디지털 시스템의 시스템 수준 통신 문제를 해결하는 거의 범용적인 솔루션으로 자리 잡고 있다.
이들은 원래 다중 컴퓨터(multicomputer)의 까다로운 통신 요구 사항을 해결하기 위해 개발되었지만, 현재는 버스를 대체하는 시스템 수준 표준 interconnection으로 자리잡고 있다. 또한 특수 목적 시스템에서의 전용 배선 역시, routing wires보다 routing packets이 더 빠르고 경제적이라는 사실이 알려지면서 interconnection network로 대체되고 있다.

1.1 Interconnection Networks에 대한 세 가지 질문

본격적으로 들어가기 전에, interconnection network에 대한 몇 가지 기본적인 질문을 살펴본다:

• Interconnection network란 무엇인가?
• 어디에서 사용되는가?
• 왜 중요한가?

Interconnection network란 무엇인가?

그림 1.1에서 볼 수 있듯, interconnection network는 단말들 사이의 데이터를 전송하는 programmable system이다. 그림에서는 T1부터 T6까지 여섯 개의 단말이 네트워크에 연결되어 있다. 예를 들어, T3이 T5로 데이터를 전송하려고 하면, 네트워크에 메시지를 보내고 네트워크가 그 메시지를 T5로 전달한다. 이 네트워크는 특정 시점마다 다른 연결을 수행하는 programmable한 특성을 갖는다. 예를 들어, 한 클럭 주기에는 T3에서 T5로 메시지를 전송하고, 다음 클럭 주기에는 동일한 자원을 사용해 T3에서 T1로 메시지를 전송할 수 있다. 이 네트워크는 여러 구성 요소 — buffers, channels, switches, controls — 로 이루어진 system이다.

이러한 정의를 만족하는 네트워크는 다양한 스케일에서 등장한다.

• On-chip network는 단일 프로세서 내의 메모리 어레이, 레지스터, 연산 유닛 사이의 데이터를 전달한다.
• Board-level, System-level 네트워크는 프로세서와 메모리, 또는 입력 포트와 출력 포트를 연결한다.
• Local-area network (LAN), Wide-area network (WAN)는 서로 떨어진 시스템을 하나의 기업 또는 전 세계적으로 연결한다.

이 책에서는 chip-level에서 system-level까지의 작은 스케일만을 다룬다. 더 큰 스케일의 네트워크는 이미 우수한 참고서들이 존재하기 때문이다. 시스템 수준 이하에서는 채널 길이가 짧고 데이터 전송 속도가 매우 높기 때문에, 대규모 네트워크와는 근본적으로 다른 해결책이 요구된다.

그림 1.1: Interconnection network의 기능적 개요. T1~T6의 단말이 양방향 채널로 네트워크에 연결되어 있다. 각 채널의 양 끝에 있는 화살표는 데이터가 양방향으로 이동할 수 있음을 나타낸다.

Interconnection network는 어디에서 사용되는가?
서로 연결해야 할 두 개 이상의 구성 요소가 있는 거의 모든 디지털 시스템에서 사용된다. 가장 일반적인 응용처는 컴퓨터 시스템과 통신 스위치이다.

• 컴퓨터 시스템에서는 프로세서와 메모리, I/O 장치와 I/O 컨트롤러를 연결한다.
• 통신 스위치 및 네트워크 라우터에서는 입력 포트를 출력 포트에 연결한다.
• 제어 시스템에서는 센서와 액추에이터를 프로세서에 연결한다.

즉, 시스템의 두 구성 요소 간에 비트를 전송하는 곳이라면 어디든 interconnection network가 존재할 가능성이 높다.

1980년대 후반까지만 해도 이러한 많은 응용은 매우 단순한 interconnection인 multi-drop bus로 구현되었다. 만약 이 책이 그 시기에 쓰였다면, 아마도 버스 설계에 관한 책이 되었을 것이다. 현재도 버스는 많은 응용에서 중요하므로, 이 책의 Chapter 22에서 별도로 다룬다.

하지만 오늘날의 고성능 시스템에서는 point-to-point interconnection network가 대부분의 연결을 담당한다. 또한 전통적으로 버스를 사용해왔던 시스템들도 매년 네트워크 방식으로 전환되고 있다.
이러한 전환은 비균등한 성능 스케일링에 기인한다. 프로세서 성능과 함께 interconnection 성능 요구도 매년 약 50%씩 증가하는 반면, 배선(wire)은 더 빨라지지 않는다. 빛의 속도나 24 게이지 구리선의 감쇠 특성은 반도체 기술이 개선되어도 나아지지 않는다. 결과적으로 버스는 요구되는 bandwidth를 따라가지 못하고 있으며, 병렬성과 더 높은 속도를 제공하는 point-to-point interconnection network가 이를 대체하고 있다.

Interconnection network가 중요한 이유는 무엇인가?
이는 많은 시스템에서 성능의 제한 요소이기 때문이다.

• 프로세서와 메모리 사이의 interconnection network는 memory latency와 memory bandwidth를 결정하며, 이는 시스템 성능의 핵심 요소이다.
• 통신 스위치에서의 interconnection network (이 문맥에서는 fabric이라 부르기도 함)는 용량(capacity) — 즉 데이터 전송률과 포트 수 — 을 결정한다.

Interconnection 요구는 배선의 물리적 한계를 훨씬 앞질러 성장하고 있기 때문에, 대부분의 시스템에서 interconnection은 치명적인 병목 요소가 되었다.

또한 interconnection network는 전용 배선(dedicated wiring)에 비해 매력적인 대안이다. 이는 낮은 duty factor를 가지는 여러 신호들이 제한된 배선 자원을 공유할 수 있게 하기 때문이다.
예를 들어, Figure 1.1에서 각 단말이 100 클럭마다 다른 모든 단말에 1워드씩 통신한다고 하자. 모든 단말쌍 사이에 전용 채널을 제공하면 30개의 단방향 채널이 필요하며, 이 채널들은 99%의 시간 동안 유휴 상태일 것이다. 대신 여섯 개의 단말을 ring network로 연결하면 6개의 채널만 필요하다 (T1→T2, T2→T3, ..., T6→T1). 이 경우 채널 수는 5배 줄고, duty factor는 1%에서 12.5%로 증가한다.

1.2 Interconnection Networks의 용도

Interconnection network 설계에 요구되는 조건을 이해하려면, 디지털 시스템에서 이것이 어떻게 사용되는지를 살펴보는 것이 유용하다. 이 섹션에서는 세 가지 일반적인 용도를 살펴보며, 각각의 응용이 네트워크 설계에 어떤 요구를 가하는지 살펴본다. 특히 다음과 같은 네트워크 파라미터를 응용에 따라 분석한다:

1. 단말의 수
2. 각 단말의 최대 대역폭 (peak bandwidth)
3. 각 단말의 평균 대역폭 (average bandwidth)
4. 요구되는 지연 시간 (latency)
5. 메시지 크기 혹은 메시지 크기의 분포
6. 예상되는 트래픽 패턴
7. 요구되는 Quality of Service
8. 요구되는 신뢰도 및 가용성

단말 수 (또는 포트 수)는 네트워크에 연결해야 할 구성 요소의 수에 해당한다. 하지만 단말 수만 아는 것으로는 부족하고, 각 단말이 네트워크와 어떻게 상호작용하는지도 알아야 한다.

각 단말은 네트워크에서 일정량의 대역폭을 요구하며, 이는 보통 bit/s로 표현된다. 특별한 언급이 없으면 단말의 입출력 대역폭은 대칭(symmetric)하다고 가정한다.

• Peak bandwidth는 단기간에 단말이 요구할 수 있는 최대 데이터율이고,
• Average bandwidth는 장기적으로 요구되는 평균 데이터율이다.

다음 섹션에서 processor-memory interconnect 설계를 통해 보여주듯, peak와 average bandwidth 모두를 아는 것이 네트워크의 구현 비용을 최소화하는 데 중요하다.

또한 네트워크가 메시지를 수신하고 전달하는 속도 외에도, 개별 메시지를 전달하는 데 걸리는 시간, 즉 메시지 지연 시간(latency) 역시 명시되어야 한다. 이상적인 네트워크는 고대역폭과 저지연을 모두 지원하지만, 이 두 가지 특성 사이에는 종종 트레이드오프가 존재한다.
예를 들어, 고대역폭을 지원하는 네트워크는 네트워크 자원을 계속 바쁘게 유지하므로, resource contention이 자주 발생한다.
즉, 여러 메시지가 동시에 동일한 공유 자원을 사용하려 하면, 하나를 제외한 나머지는 해당 자원이 사용 가능해질 때까지 기다려야 하므로 latency가 증가한다. 반대로, 대역폭 요구를 줄이면 자원 사용률이 낮아지므로 latency도 감소할 수 있다.

Message size, 즉 메시지의 비트 길이도 중요한 설계 고려 요소이다. 메시지가 작을 경우, 네트워크 오버헤드가 성능에 더 큰 영향을 미치게 된다. 반면 메시지가 크면 오버헤드를 메시지 길이에 걸쳐 분산시켜 감쇠시킬 수 있다. 많은 시스템에서는 여러 가지 가능한 메시지 크기가 존재한다.

각 단말에서 보낸 메시지가 가능한 목적지 단말 전체에 어떻게 분포되는가를 트래픽 패턴(traffic pattern)이라 한다. 예를 들어, 각 단말이 모든 다른 단말에 동일한 확률로 메시지를 보내는 경우를 무작위 트래픽 패턴(random traffic pattern)이라 한다. 반대로 단말들이 주로 가까운 단말에만 메시지를 보내는 경향이 있다면, underlying network는 이러한 공간적 지역성(spatial locality)을 활용하여 비용을 줄일 수 있다. 그러나 어떤 네트워크에서는 임의의 트래픽 패턴에서도 사양이 유지되는 것이 중요하다.

일부 네트워크에서는 QoS (Quality of Service) 요구사항도 있다. 대략적으로 QoS란 특정 서비스 정책 하에서 자원을 공정하게 분배하는 것이다. 예를 들어, 여러 메시지가 동일한 네트워크 자원을 놓고 경쟁할 때, 이를 해결하는 방식은 여러 가지다. 메시지가 해당 자원을 기다린 시간에 따라 선착순(First-Come, First-Served) 방식으로 처리할 수도 있고, 네트워크 내에서 가장 오래 있었던 메시지에 우선순위(priority)를 줄 수도 있다. 어떤 자원 할당 정책을 선택할지는 네트워크에서 요구하는 서비스에 따라 달라진다.

마지막으로, 신뢰도(reliability)와 가용성(availability)도 interconnection network의 설계에 영향을 준다.

• 신뢰도란 메시지를 올바르게 전달하는 네트워크의 능력을 말한다. 대부분의 경우 메시지는 100% 전달되어야 하며 손실이 없어야 한다. 이를 실현하기 위해 에러 검출 및 수정 하드웨어, 상위 소프트웨어 프로토콜, 또는 이들의 조합을 사용할 수 있다.
• 일부 경우, 이후에 설명할 packet switching fabric에서는 극소수의 메시지가 손실되는 것을 허용할 수도 있다.

네트워크의 가용성은 전체 시간 중 네트워크가 정상적으로 작동한 비율을 의미한다. 인터넷 라우터의 경우, 일반적으로 99.999% (5 nines) 가용성이 요구되며, 이는 연간 총 다운타임이 5분 미만임을 의미한다. 그러나 네트워크를 구성하는 부품은 종종 분당 여러 번 고장나기도 하므로, 이러한 수준의 가용성을 달성하려면 네트워크는 장애를 감지하고 신속하게 복구하면서도 동작을 지속해야 한다.

1.2.1 Processor-Memory Interconnect

그림 1.2는 processor와 memory를 연결하기 위한 interconnection network의 두 가지 구조를 보여준다.

• (a) Dance-hall 구조는 P개의 프로세서와 M개의 메모리 뱅크를 interconnection network로 연결한다.
• (b) Integrated-node 구조는 processor와 memory를 하나의 노드에 통합하고, 이 로컬 메모리에는 switch C를 통해 직접 접근할 수 있게 한다.

Dance-hall이라는 이름은 구식 댄스홀처럼, 프로세서들이 네트워크 한쪽에 줄지어 서고, 메모리들이 반대쪽에 줄지어 서는 배치를 닮았기 때문이다.

Table 1.1은 이 두 구성에서 네트워크에 요구되는 파라미터를 요약한 것이다.

예를 들어 Cray T3E와 같이 최대 구성 시 2,176개의 processor ports를 가진 경우도 있으며, 단일 프로세서 시스템에서는 1개의 포트만 필요하다.
64~128개의 프로세서를 가진 구성은 고급 서버에서 흔하며, 이 수는 시간이 갈수록 증가하는 추세다.

• Integrated-node 구성에서는 각 processor port가 memory port 역할도 한다.
• 반면 dance-hall 구성에서는 memory port 수가 processor port보다 훨씬 많다. 예: 어떤 벡터 프로세서는 32개의 processor port가 4,096개의 memory bank에 접근한다. 이는 memory bandwidth를 극대화하고 bank conflict(동일한 bank에 여러 프로세서가 동시에 접근하는 경우)를 줄이기 위한 것이다.

현대의 마이크로프로세서는 초당 약 10억 개의 명령어를 실행하며, 각 명령어는 memory에서 64비트 word 두 개를 요구할 수 있다 (하나는 명령어 자체, 다른 하나는 데이터). 이 중 하나가 캐시에 없으면 일반적으로 8-word block을 memory에서 가져온다. 만약 매 cycle마다 2 word를 memory에서 가져와야 한다면 16GB/s의 bandwidth가 필요하다.

다행히도:

• 모든 명령어가 메모리 참조를 하는 것은 아니며 (약 1/3),
• cache hit ratio가 높아서 실제 memory 접근 수는 줄어든다.

따라서 평균 bandwidth는 훨씬 낮아져 보통 400MB/s 수준이 된다. 하지만 burst traffic을 처리하기 위해서는 8GB/s의 peak bandwidth가 여전히 필요하다.
만약 peak bandwidth를 너무 제한하면 갑작스러운 요청이 발생했을 때 네트워크 포트가 막혀 serialization이 발생하고, 이는 지연(latency)을 증가시킨다. 이 현상은 막힌 싱크대가 천천히 물을 빼내는 것에 비유할 수 있다.

또한, memory latency는 processor 성능에 민감한 영향을 미친다. Table 1.1에서는 기본 메모리 시스템의 latency를 100ns로 보고 있는데, 네트워크가 추가로 100ns를 더한다면 실효 메모리 지연이 2배가 된다.

캐시에 없는 load/store 명령어는 read-request 또는 write-request packet으로 변환되어 네트워크를 통해 해당 memory bank로 전송된다.

• Read-request packet: 읽을 memory address 포함
• Write-request packet: 주소 + 데이터 word 또는 캐시라인 포함

memory bank는 요청을 수행한 후, 응답 packet을 다시 보낸다 (read-reply 또는 write-reply).

이 시점에서, message와 packet을 구분하기 시작한다.

• Message는 processor 또는 memory와 네트워크 간의 전송 단위이고,
• Packet은 그 message가 네트워크 내부에서 분할되거나 고정 길이로 변환된 형태이다.

Processor-memory interconnect에서는 message와 packet이 1:1 대응한다고 가정할 수 있다.

그림 1.3: 두 개의 packet format

• Read-request / Write-reply: 64비트 헤더 + 주소

Read-reply / Write-request: 위의 64비트 정보 + 512비트 데이터 (캐시라인) = 576비트

이러한 interconnect는 QoS를 요구하지 않는다. 그 이유는 시스템이 자체 조절(self-throttling) 메커니즘을 갖기 때문이다. 네트워크 혼잡이 발생하면 요청 지연이 늘어나고, processor는 응답을 기다리며 유휴 상태가 된다. 이로 인해 새로운 요청이 줄어들고 혼잡이 완화된다. 이런 안정화 특성 덕분에 QoS는 필요하지 않다.

하지만 신뢰성(reliability)은 필수이다.

• memory request/reply packet이 절대 손실되면 안 된다.
• 손실되면 해당 memory operation이 무한히 대기 상태가 되어, 최소한 사용자 프로그램이 crash되고, 심하면 시스템 전체가 다운될 수 있다.

신뢰성을 갖추기 위해, 일부 시스템은 acknowledgment 기반 재전송 프로토콜을 쓸 수 있다 (자세한 내용은 Chapter 21 참조). 하지만 이는 latency를 증가시켜 processor-memory interconnect에는 적합하지 않다.

이러한 시스템은 보통 가용성 99.9% ~ 99.999% 수준을 요구한다.

1.2.2 I/O Interconnect

그림 1.4: 일반적인 I/O 네트워크는 여러 개의 host adapter(HA)를 더 많은 수의 I/O 디바이스(예: 디스크 드라이브)에 연결한다.

I/O 네트워크는 granularity와 timing 면에서 processor-memory 네트워크와 다르다. 특히 latency에 대한 관용성 증가는 네트워크 설계를 완전히 다른 방향으로 이끈다.

디스크 작업은 일반적으로 4Kbyte 이상의 sector 단위로 수행된다. 디스크의 회전 지연(rotational latency)과 헤드 이동 시간 때문에, 섹터 하나를 접근하는 데 걸리는 latency는 수 밀리초에 달할 수 있다. 디스크 읽기 작업은 host adapter에서 디스크 주소(device, sector)와 메모리 블록 주소를 지정한 control packet을 전송하면서 시작된다. 디스크는 이 요청을 수신하고 헤드를 해당 섹터로 이동시킨 뒤, 해당 sector를 읽고, 지정된 메모리 블록으로의 response packet을 host adapter에 보낸다.

표 1.2 I/O interconnection network의 파라미터

a) 일부 메시지 손실은 허용된다. 실패한 메모리 접근보다 실패한 I/O 작업의 복구가 더 유연하게 처리되기 때문이다.

디스크 포트의 peak-to-average bandwidth ratio는 매우 크다. 디스크가 연속된 sector를 전송할 때는 200MB/s의 속도로 데이터를 읽을 수 있지만, 실제로는 각 sector 간에 헤드 이동 시간이 평균 5ms 이상 걸려서, 평균 데이터 속도는 1MB/s 이하로 낮아진다. Host 포트는 64개의 디스크 포트 트래픽을 집계하므로 이보다는 안정적인 대역폭을 가진다.

이처럼 peak과 average bandwidth 차이가 큰 경우, 모든 디바이스의 최대 대역폭을 동시에 지원하는 네트워크를 설계하면 비용이 매우 높아진다. 반대로 평균 대역폭만 지원하도록 설계하면, processor-memory 예시처럼 serialization latency 문제가 생긴다. 따라서 여러 디바이스의 요청을 집계 포트(aggregate port)로 concentration하는 방식이 효과적이다. 이로 인해 평균 bandwidth 수요는 커지지만, 실제로 동시에 최고 대역폭을 요구하는 디바이스는 극소수에 불과하므로 과도한 serialization 없이 저비용 구현이 가능하다.

메시지의 payload는 이중 분포(bimodal)를 가지며, 두 가지 크기 간의 차이가 크다.

• 짧은 32바이트 메시지: read 요청, write 완료 ack, 디스크 제어용
• 긴 메시지 (예: 4Kbyte, 실제는 8Kbyte 포함됨): read-reply, write-request 등

디스크 작업은 본질적으로 latency가 크고, 전송 단위가 크기 때문에, 이 네트워크는 latency에 민감하지 않다. 예를 들어, latency가 10μs로 증가해도 성능 저하는 무시할 수 있는 수준이다. 이러한 관용성 덕분에 processor-memory에 비해 효율적인 네트워크를 훨씬 쉽게 구축할 수 있다.

한편, 클러스터 기반 병렬 컴퓨터에서 사용하는 inter-processor 통신 네트워크는 bandwidth와 granularity 면에서 I/O 네트워크와 유사하므로 따로 다루지 않는다. 이러한 네트워크는 system-area network (SAN)라고 불리며, I/O 네트워크와의 주요 차이는 latency에 더 민감하다는 점이다 (보통 몇 마이크로초 이하 요구).

한편, 디스크 스토리지를 기업의 핵심 데이터를 저장하는 데 사용하는 경우, 매우 높은 가용성이 요구된다. 스토리지 네트워크가 멈추면 곧 비즈니스 전체가 중단되기 때문이다. 이 때문에 0.99999 (five nines) 수준 — 연간 다운타임 5분 이하 — 이 일반적이다.

1.2.3 Packet Switching Fabric

Packet switching fabric은 통신 네트워크 스위치 및 라우터에서 버스와 크로스바를 대체하는 역할을 한다. 이 경우 interconnection network는 보다 큰 네트워크(IP 기반의 LAN 또는 WAN)의 라우터 내부 요소로 동작한다.

그림 1.5: 스위칭 패브릭으로 interconnection network를 사용하는 네트워크 라우터. 여러 line card 간의 패킷 전송을 담당한다.

대규모 네트워크 채널 (보통 2.5Gbps 또는 10Gbps 광섬유)을 종료하는 여러 line card들이 있고, 각 라인카드는:

1. 패킷을 받아서 목적지를 파악하고,
2. QoS 정책 준수 여부를 검사하고,
3. 패킷의 특정 필드를 재작성하고,
4. 통계 정보를 업데이트한 후,
5. 해당 패킷을 fabric으로 전달한다.

fabric은 이 패킷을 출발지 line card에서 목적지 line card로 전송하는 역할을 수행한다. 목적지 line card는 해당 패킷을 큐에 저장하고, 이후 출력 채널로 송신하도록 스케줄링한다.

표 1.3 Packet switching fabric의 파라미터

라우터에서 사용하는 프로토콜에 따라 패킷 크기가 달라지지만,
예를 들어 IP의 경우 40바이트~64Kbytes까지 다양하며, 일반적으로는 40, 100, 1,500바이트 패킷이 많다. 이처럼 다른 예시들과 마찬가지로, 이 네트워크도 짧은 제어 메시지와 큰 데이터 전송 간의 분리가 있다.

스위칭 패브릭은 processor-memory나 I/O 네트워크처럼 self-throttling 하지 않다. 각 line card는 네트워크 혼잡과 무관하게 계속 패킷을 전송하며, 동시에 일부 패킷 클래스에는 보장된 bandwidth를 제공해야 한다. 이를 위해 fabric은 non-interfering해야 한다. 즉:

• a로 가는 트래픽이 많더라도,
• b로 가는 트래픽의 bandwidth를 침해하지 않아야 한다.
• 이는 a와 b 간 트래픽이 자원을 공유하더라도 마찬가지다.

이런 비간섭성 요구는 fabric 구현에 특별한 제약 조건을 부과한다.

흥미로운 점은, 일부 경우 극히 낮은 확률의 패킷 손실은 허용 가능하다는 것이다. 예를 들어:

• 입력 광섬유에서의 비트 오류 (10⁻¹² ~ 10⁻¹⁵ 확률),
• line card 큐 오버플로우 등,
  이미 다른 이유로 인해 패킷이 손실될 수 있기 때문에,
  내부 네트워크 bit error와 같은 매우 드문 상황에서는 패킷을 드롭해도 무방하다.
  단, 이 손실률은 다른 원인보다 훨씬 낮아야 한다.

이는 processor-memory interconnect와는 대조된다. 이 경우 패킷 1개라도 손실되면 시스템 전체가 정지될 수 있기 때문이다.

1.3 Network Basics

특정 응용 분야(앞에서 설명한 바와 같은)의 성능 사양을 충족시키기 위해, 네트워크 설계자는 topology, routing, flow control을 구현함에 있어 기술적 제약 내에서 작업해야 한다. 앞에서 언급했듯, interconnection network의 효율성의 핵심은 통신 자원이 공유된다는 점이다. 각 terminal 쌍마다 전용 채널을 만드는 대신, interconnection network는 공유 채널로 연결된 공유 router node 집합으로 구현된다. 이 노드들의 연결 패턴이 곧 topology를 정의한다.

메시지는 출발 terminal에서 목적지 terminal까지 여러 shared channel과 node를 거쳐 전달된다. 좋은 topology는 패키징 기술의 특성 — 예: 칩의 핀 수, 캐비닛 간 연결 가능한 케이블 수 — 을 잘 활용하여 network bandwidth를 극대화할 수 있어야 한다.

Toplogy가 정해지면, 메시지가 목적지에 도달하기까지의 가능한 경로(노드와 채널의 시퀀스)는 여러 가지가 될 수 있다. Routing은 메시지가 어떤 경로를 실제로 따를지를 결정한다. 좋은 경로 선택은 경로 길이(보통 노드 수나 채널 수로 측정)를 최소화하고, 동시에 공유 자원에 걸리는 부하(load)를 고르게 분산시켜야 한다.

• 경로가 길수록 latency가 늘어나고,
• 자원 중 어떤 것은 과하게 사용되고, 다른 것은 유휴 상태인 load imbalance가 발생하면 network의 총 bandwidth는 줄어든다.

Flow control은 시간 흐름에 따라 어떤 메시지가 어떤 network 자원을 사용할지를 결정한다. 자원 사용률이 증가할수록 flow control의 중요성은 커진다. 좋은 flow control은 최소 지연으로 packet을 전달하면서, 높은 부하 상태에서도 자원을 놀리지 않는다.

1.3.1 Topology

Interconnection networks는 router node들과 channel들로 구성되며, topology는 이들의 배치 방식을 의미한다. Topology는 도로 지도에 비유할 수 있다. Channel은 자동차가 다니는 도로처럼 packet을 한 router node에서 다른 router node로 운반한다. 예를 들어 Figure 1.6에 나온 network는 16개의 노드로 구성되며, 각 노드는 4개의 이웃과 양방향 연결(총 8개의 채널)되어 있다. 이 네트워크는 torus topology이다. 각 노드는 terminal과 직접 연결된 direct network 구성이다.

좋은 topology는 사용 가능한 패키징 기술의 특성을 활용하여 최소 비용으로 응용의 bandwidth와 latency 요구를 충족시킨다. Topology는 시스템 중간(bisection)을 가로지르는 bisection bandwidth를 최대한 활용해야 한다.

Figure 1.6: 4×4 torus (또는 4-ary 2-cube) topology.
각 노드는 4개의 이웃과 각각 송수신 채널로 연결되어 총 8개의 채널을 가진다.

Figure 1.7은 Figure 1.6의 네트워크를 실제로 어떻게 패키징할 수 있는지를 보여준다.

• 4개의 노드를 하나의 printed circuit board (PCB)에 배치하고,
• 4개의 보드를 backplane 보드로 연결한다 (PC에서 PCI 카드가 motherboard에 꽂히듯).

이 시스템에서 bisection bandwidth는 backplane을 통해 전달될 수 있는 최대 bandwidth이다.

• backplane이 256개의 신호선(signal)을 가진다고 가정하고,
• 각 signal이 1Gbps 속도로 동작한다면, 전체 bisection bandwidth는 256Gbps이다.

Figure 1.7: 16-node torus topology의 패키징.
4개의 PCB가 backplane을 통해 연결된다. backplane의 너비를 가로지르는 256개 신호선이 이 시스템의 bisection bandwidth를 결정한다.

다시 Figure 1.6을 보면, 중간을 가로지르는 unidirectional channel이 총 16개이다. (그림상의 선 하나는 양방향 채널 2개를 의미함) 따라서 bisection bandwidth를 포화시키려면 각 채널은 256/16 = 16 signals를 가져야 한다. 한편, 각 노드는 단일 IC 칩에 패키징되며, 칩은 최대 128개의 핀만 사용할 수 있다. 이 topology는 노드당 8개 채널이므로, 각 채널당 할당 가능한 핀 수는 128/8 = 16 signals이다.
→ 핀 제한과 포화 조건이 일치하는 이상적인 구성이다.

반면, Figure 1.8과 같이 16-node ring topology를 고려해보자.

• 노드당 4개 채널만 존재하므로 핀 제한은 128/4 = 32 signals/channel이 된다.
• bisection을 통과하는 채널은 4개이므로 이상적인 설계는 채널당 256/4 = 64 signals/channel이지만,
• 핀 제한으로 인해 실제 채널 폭은 32 signal로 제한된다.
  → 결국, ring topology는 torus topology의 절반 bandwidth만 제공한다.

Figure 1.8: 동일한 기술 제약 조건 하에서 ring topology는 torus보다 낮은 throughput을 가지지만 latency는 더 낮을 수 있다.

그러나 bandwidth만이 topology 선택의 기준은 아니다.
다른 응용에서 필요한 bandwidth가 16Gbps 수준으로 낮지만 latency가 중요하다면, 4096-bit의 긴 packet을 사용하고 있다면,
→ 작은 hop 수와 낮은 serialization latency의 균형을 맞추는 topology가 필요하다.

• Hop count: 메시지가 목적지까지 평균적으로 거치는 노드/채널 수
• Node degree를 높이면 hop count는 줄지만,
• 채널 수가 늘어나면 채널 폭은 좁아지고, 긴 패킷은 serialization latency가 커진다.

예를 들어,

• random traffic을 가정하면, torus의 평균 거리 = 2 hops, ring = 4 hops
• hop 당 20ns라면 torus: 40ns, ring: 80ns

4096-bit 패킷 전송 시 serialization latency

• ring (32 signals): 4096 / 32 = 128 cycles → 128ns
• torus (16 signals): 4096 / 16 = 256 cycles → 256ns

→ ring의 총 latency: 80 + 128 = 208ns
→ torus의 총 latency: 40 + 256 = 296ns

결론: 긴 패킷에서는 오히려 ring topology가 latency 면에서 우수할 수 있다.

요약: 모든 응용에 적합한 최적의 topology는 없다.
제약 조건과 요구사항에 따라 적절한 topology가 달라진다.

1.3.2 Routing

Routing은 source terminal node에서 destination terminal node까지의 경로를 결정한다.
경로는 channel들의 순서 집합
P = {c₁, c₂, ..., cₖ} 로 정의되며,

• cᵢ의 출력 노드 = cᵢ₊₁의 입력 노드
• c₁의 입력 = source
• cₖ의 출력 = destination

어떤 네트워크에서는 source→destination 경로가 유일할 수도 있지만, Figure 1.6의 torus network처럼 경로가 여러 개 존재할 수도 있다. 이럴 경우, 좋은 routing 알고리즘은 어떤 traffic pattern에서도 채널 간 부하를 고르게 분산해야 한다.

• topology는 roadmap,
• routing은 네트워크 교차로에서 방향을 정하는 운전자의 turning decision이다.
• 부하 균형을 위해, 일부 경로에 트래픽이 몰리지 않도록 해야 한다.

Figure 1.9(a): node 01에서 node 22로 가는 dimension-order routing
→ x방향으로 먼저 이동 후, y방향으로 이동 (01 → 21 → 22).
→ 최소 경로 (min-hop). 이 경우 가능한 최소 경로가 총 6개 존재한다.

Figure 1.9(b): node 00 → 22 경로 예시.
→ 총 5 hops를 거치는 non-minimal route (최소는 3 hop).

Dimension-order routing은 간단하고 minimal하지만, 일부 traffic pattern에서는 심각한 load imbalance를 유발할 수 있다.
예를 들어, Figure 1.9(a)에서 node 11에서 node 20으로 가는 또 다른 dimension-order 경로를 추가한다고 하자. 이 경로 역시 node 11에서 node 21로 가는 채널을 사용하므로, 해당 채널의 부하(load)가 2배가 된다.

Channel load는 terminal node들이 해당 채널을 통해 보내려고 하는 평균 bandwidth를 의미한다. 이 load를 terminal이 네트워크에 주입할 수 있는 최대 rate로 정규화하면, 해당 채널의 load는 2가 된다.
더 나은 routing 알고리즘을 사용하면 이 값을 1로 줄일 수 있다. Dimension-order routing은 특정 채널에 불필요한 중복 부하를 발생시키므로, 이 traffic pattern 하에서 네트워크의 전체 bandwidth는 최대의 절반에 불과하다.

일반적으로 deterministic routing algorithm — 즉 source-destination 쌍마다 고정된 단일 경로를 선택하는 알고리즘 — 은 이러한 load imbalance로 인해 낮은 bandwidth를 보이는 경향이 있다.
Routing 알고리즘 설계와 관련된 이와 같은 이슈는 Chapters 8–10에서 더 자세히 다룬다.

1.3.3 Flow Control

Flow control은 packet이 경로를 따라 진행함에 따라 자원의 할당을 관리한다. 대부분의 interconnection network에서 핵심 자원은 channel과 buffer이다.
Channel은 노드 간에 packet을 운반하는 역할을 하며, Buffer는 각 노드 내에 구현된 저장 공간(레지스터나 메모리 등)으로, packet이 다음 자원을 기다리는 동안 임시로 저장된다.

이전의 아날로지를 이어서 보면:

• Topology는 지도,
• Routing은 교차로에서의 steering 결정,
• Flow control은 신호등이다.
  → 즉, 차(=packet)가 다음 도로(channel)로 진행해도 되는지, 혹은 다른 차를 위해 parking lot(buffer)으로 비켜야 하는지를 결정한다.

Figure 1.9:
(a) Dimension-order routing: x 방향 → y 방향
(b) Non-minimal route: 최소 경로보다 더 많은 hop을 거친다

Topology와 Routing의 잠재적 성능을 실현하려면, Flow control 전략은 자원 충돌(resource conflict)을 피해야 한다.
예: 어떤 packet이 비어 있는 채널을 사용할 수 있음에도, 혼잡한 채널 때문에 막힌 다른 packet이 점유 중인 buffer를 기다리느라 진행하지 못하는 상황은 피해야 한다.
→ 이 상황은, 좌회전 하려는 차 때문에 직진하려는 차가 막히는 것과 같다.
→ 해결책은 도로에 좌회전 전용 차선을 추가하는 것처럼, 자원 의존을 분리해주는 것이다.

좋은 flow control은 공정하고(fair), deadlock을 피해야 한다.

• 공정하지 않으면 어떤 packet은 무한정 대기할 수 있으며,
• Deadlock은 여러 packet이 서로 자원을 기다리며 순환적으로 막혀 있는 상태를 의미한다.
  → 도로에서의 gridlock에 해당한다.

Flow control 방식은 종종 시간-공간 다이어그램(time-space diagram)으로 표현된다.

Figure 1.10: Flow control 비교

• (a) Store-and-forward: 각 채널마다 packet 전체(5 flits)가 전달되어야 다음 채널로 진행 가능
• (b) Cut-through: 각 flit이 도착하는 대로 다음 채널로 바로 진행, pipelining

• 수평축: 시간(cycle)
• 수직축: 공간(channel ID)
• Flit (flow control digit): flow control 수준에서 가장 작은 단위
  → flit을 고정된 크기로 정하면 router 설계가 간단해지고, 길이가 일정하지 않은 packet도 처리할 수 있다.

→ Flow control 방식은 latency에 큰 영향을 미친다.

Flow control의 자세한 내용은 Chapters 12–13,
관련 문제들 (deadlock, livelock, tree saturation, QoS 등)은 Chapters 14–15에서 다룬다.

1.3.4 Router Architecture

Figure 1.11: router의 block diagram

• 입력 채널마다 buffer
• crossbar switch
• allocator

Figure 1.6에 나온 16개의 노드 중 하나의 내부를 단순화하여 나타낸 그림이다.

• 각 입력 채널에는 buffer가 연결되어 있고,
• buffer에 들어온 flit은 경로 상 다음 노드(router)의 buffer 공간이 확보되면
  → crossbar switch에 대한 접근 권한을 요청한다.

Crossbar switch는 어느 입력 buffer든지 어느 출력 채널로든 연결할 수 있으나,

• 입력 하나는 출력 하나에만, 출력 하나도 입력 하나에만 연결 가능하다.

Allocator는 crossbar와 공유 자원에 대한 요청을 처리한다.
→ flit이 다음 router로 진행하려면,

1. 다음 노드의 buffer 공간 확보
2. 다음 채널의 bandwidth 확보
3. crossbar 통과 권한 확보

Router architecture는 Chapters 16–21에서 상세히 다룬다.

1.3.5 Performance of Interconnection Networks

Interconnection network의 성능은 보통 latency vs. offered traffic curve로 설명된다.

Figure 1.12: offered traffic(수평축)에 따른 평균 latency(수직축)

• Latency: packet의 첫 비트가 source terminal에 도착한 시점부터,
  마지막 비트가 destination terminal에 도착한 시점까지 걸린 시간
• Offered traffic: 각 source terminal이 생성하는 평균 트래픽 (bits/s)

이 곡선을 정확히 얻기 위해선 트래픽 패턴 (예: random traffic)도 명시해야 한다.
→ 이 곡선은 정확하긴 하나, 폐쇄형 수식이 없으며 discrete-event simulation으로 계산된다.

설계 초기 단계에서는 topology, routing, flow control 관점에서 점진적으로 성능을 이해하는 방식이 유용하다.

Zero-load latency는 네트워크에서 경쟁 없이 packet이 전달될 때의 최소 평균 지연 시간이다.

• 구성 요소: serialization latency + hop latency

예:

• topology = torus (Figure 1.6)
• L = 512 bits,
• channel bandwidth = b = 16 Gbps
• routing: minimal, random traffic
  → serialization latency = L/b = 32ns
  → 평균 hop 수 = Hₘᵢₙ = 2
  → router latency tᵣ = 10ns
  → hop latency = 2 × 10 = 20ns
  → 최소 latency = 32 + 20 = 52ns

Routing 알고리즘이 실제로 사용하는 hop 수 Hₐᵥg를 고려하면, 이보다 큰 latency가 된다 (Hₐᵥg ≥ Hₘᵢₙ).
또한 flow control이 추가로 성능을 저하시킬 수 있다.

예: store-and-forward flow control에서는 latency = Hₐᵥg × tᵣ

Figure 1.12 요약:

• 낮은 traffic에서는 latency가 T₀ (zero-load latency)에 수렴
• saturation throughput λₛ에서 latency가 무한대로 발산
• λₛ는 topology 한계 2Bc/N 및 routing 한계 Θᴿ로 제한됨

앞서 설명한 Figure 1.12에서, 실제 zero-load latency T₀는 topology, routing, flow control에 의해 결정되는 제약을 모두 포함한다. 이러한 점진적으로 정밀해지는 latency의 상한들은 Figure 1.12에서 수평 비대칭선(horizontal asymptote)으로 표시된다.

비슷한 방식으로 throughput(처리율)에 대해서도 상한을 설정할 수 있다.

• Source는 일정량의 traffic을 network에 제공하지만,
• Throughput, 또는 accepted traffic은 destination terminal에 성공적으로 전달된 데이터율(bits/s)이다.

예를 들어, random traffic을 가정하면 전체 traffic의 절반이 network의 bisection을 통과해야 한다.

• bisection은 16개 채널, 총 bandwidth B_c = 256 Gbps
• node당 traffic 한계 = 2B_c / N = 32 Gbps (N=16)

이는 traffic이 bisection을 균등하게 분산시킨다는 이상적인 가정 하에서만 성립한다.

→ 실제 routing 알고리즘 R의 효과를 고려한 throughput Θ_R은 불균형이 존재하면 이보다 낮을 수 있다 (Θ_R ≤ 2B_c / N)
→ Flow control이 자원 의존성 때문에 채널을 유휴 상태로 만든다면, 실제 saturation throughput λ_s는 Θ_R보다도 훨씬 낮을 수 있다.

이러한 throughput의 3단계 상한은 Figure 1.12에서 수직 비대칭선(vertical asymptote)으로 표시된다.

이렇게 topology → routing → flow control로 점진적으로 성능을 분석하는 방식은 각 설계 요소가 성능에 어떻게 영향을 미치는지 불필요한 복잡성 없이 확인할 수 있게 해준다.
예: topology 선택이 latency에 미치는 영향은, routing과 flow control을 따로 고려하지 않고도 파악 가능하다.

반면, 성능 분석을 한 번에 모두 고려하려 하면 개별 설계 선택이 끼치는 영향이 흐려진다.

이러한 성능 모델링의 점진적 접근법을 수립한 후, 전체적인 관점에서의 성능 분석은 Chapters 23–25에서 다룬다.
이들 챕터에서는:

• 성능 측정에서의 미묘한 문제
• queueing theory 및 probability theory 기반의 분석 기법
• simulation을 통한 성능 측정 방법
• 예시 측정 결과들을 설명한다.

1.4 History

Interconnection network는 수십 년에 걸쳐 발전해 온 풍부한 역사를 가지고 있다. 발전 경로는 크게 세 가지 병렬적 흐름으로 진행되었다:

1. Telephone switching networks
2. Inter-processor communication
3. Processor-memory interconnect

Telephone switching networks

전화가 등장한 이래로 존재해온 시스템이다. 초기 telephone network는 전기기계식 crossbar 또는 step-by-step switch로 구축되었으며,
1980년대까지도 많은 지역 전화 교환기는 여전히 electro-mechanical relay로 구성되어 있었다. 반면, 장거리 통화용(toll) switch는 이미 전자식, 디지털화가 완료되었다.

주요 발전 사례:

• 1953년: Clos network (non-blocking multistage)
• 1962년: Beneš network
  → 현재도 많은 대형 telephone switch는 Clos 또는 Clos 기반 네트워크로 구현된다.

Inter-processor interconnection networks

초기의 processor 간 연결은 2D 배열 내 이웃한 processor의 레지스터를 직접 연결하는 방식이었다.
예: 1962년 Solomon machine [172] — 이들 초기 네트워크는 routing 기능이 없었기 때문에, 이웃이 아닌 processor와 통신하려면 중간 processor가 명시적으로 relay해야 했다.
→ 이는 성능 저하와 프로그래밍 복잡성 증가로 이어졌다.

1980년대 중반부터는 processor 개입 없이 메시지를 forwarding할 수 있는 router chip이 등장했다.
예: torus routing chip [56]

Topology 측면에서는 시간 흐름에 따라 다양한 유행이 있었다:

• 초기 (Solomon, Illiac, MPP 등): 2D mesh 또는 torus → 물리적 규칙성 때문
• 1970년대 후반부터: binary n-cube (hypercube) → low diameter
  → 대표 기기: Ametek S14, Cosmic Cube, nCUBE, Intel iPSC 시리즈

하지만 1980년대 중반 이후 실제 패키징 제약 하에서는 low-dimensional network가 hypercube보다 우수하다는 사실이 밝혀졌고,
→ 다시 대부분의 시스템이 2D 또는 3D mesh/torus로 회귀하였다.

대표 기기:

• J-machine [138]
• Cray T3D, T3E
• Intel DELTA
• Alpha 21364

최근에는 message 길이에 비해 router chip의 핀 대역폭(pin bandwidth)이 높아지면서, node degree가 높은 topology인 butterfly, Clos network 사용이 다시 증가하고 있다.

Processor-memory interconnect

1960년대 말부터 등장.
→ 병렬 프로세서 시스템에서 어떤 processor든지 어떤 memory bank에 접근할 수 있도록 하기 위해 alignment network를 도입함.

• 소형 시스템: crossbar 사용
• 대형 시스템: butterfly topology, dance-hall 구성

이러한 방식은 1980년대에도 많은 shared-memory parallel processor에서 활용되었다.

세 흐름의 통합

1990년대 초 이후, processor-memory와 inter-processor network 설계의 차이는 거의 사라졌다.
→ 동일한 router chip이 양쪽에 사용되고 있음
→ telephone에서 사용되던 Clos 및 Beneš network도 fat-tree topology 형태로 multiprocessor network에 적용되고 있다 [113]

이 역사에서는 주로 topology에 초점을 맞췄지만, routing과 flow control도 동시에 발전해왔다.

• 초기 routing chip: deterministic routing, circuit-switching 또는 store-and-forward packet switching 사용
• 이후: adaptive routing, deadlock avoidance, virtual-channel flow control 등장

1.5 Organization of this Book

다음 장에서는 먼저 하나의 완전한 interconnection network를 topology부터 logic gate 수준까지 설명한다.
→ 전체적인 구조를 먼저 보여주고, 이후에 세부로 들어가는 방식이다.

나머지 챕터들은 5개 주요 분야로 나뉘어 구성되어 있다:

1. Topology
2. Routing
3. Flow Control
4. Router Architecture
5. Performance

각 분야는 여러 개의 챕터로 구성되며,

• 첫 챕터는 기본 개념,
• 이후 챕터는 고급 주제를 다룬다.