라우팅은 주어진 topology 내에서 source node에서 destination node로 가는 경로를 선택하는 과정이다. 네트워크의 topology, 즉 지도와 같은 구조가 정해지면, 그다음은 그 지도에서 목적지까지 가는 길을 고르는 것이 라우팅이다. Topology가 네트워크의 이상적인 성능을 결정한다면, 라우팅은 이 성능 중 얼마나 실제로 구현되는지를 결정하는 두 가지 핵심 요소 중 하나이다. 나머지 하나는 12장과 13장에서 다룰 flow control이다.
라우팅 알고리즘은 여러 이유에서 중요하다. 좋은 라우팅 알고리즘은 permutation traffic과 같은 비균일 트래픽 패턴이 있어도 네트워크의 채널들 간 부하를 고르게 분산시킨다. 채널 부하가 균형을 이룰수록 네트워크의 throughput은 이상적인 값에 가까워진다. 하지만 의외로, 현재 사용 중인 많은 router들이 부하를 고르게 분산하는 데 실패하고 있다. 대부분의 경우, 각 노드 쌍 사이의 트래픽은 단일하고 미리 정해진 경로를 따른다. 이런 라우팅 알고리즘은 비균일 트래픽 상황에서 큰 부하 불균형을 유발할 수 있으며, 이로 인해 throughput이 떨어진다. 그럼에도 불구하고 이런 라우팅 방식이 사용되는 이유는 또 다른 중요한 라우팅 알고리즘의 특성인 짧은 경로 길이를 최적화하기 위함이다.
잘 설계된 라우팅 알고리즘은 경로 길이를 가능한 짧게 유지하여 hop 수를 줄이고, 메시지의 전체 latency를 낮춘다. 하지만 때로는 minimal routing(항상 최단 경로를 선택하는 방식)이 부하 균형과 throughput 향상과 충돌할 수 있다. 특히 oblivious routing 알고리즘에서는 모든 트래픽 패턴에 대해 부하 균형을 맞추려면 전체 메시지의 평균 경로 길이를 늘릴 수밖에 없다. 반대로 평균 경로 길이를 줄이면 부하 균형이 무너진다. Oblivious 알고리즘은 현재 트래픽 패턴을 고려하지 않기 때문에 이런 tradeoff가 생긴다. 이 알고리즘들은 9장에서 자세히 다룬다.

- 1. Greedy Routing
- 방법: 목적지까지의 최단 거리 방향으로 항상 라우팅함.
- 예: 노드 0에서 노드 3은 시계방향, 노드 0에서 노드 5는 반시계방향.
- 거리가 같을 경우 무작위로 선택.
- 특징: 경로는 짧지만, 부하 분산이 되지 않아 특정 방향에 트래픽이 몰릴 수 있음.
- Tornado traffic에서 throughput: 0.33
2. Uniform Random Routing- 방법: 패킷마다 양방향 중 무작위로 한 방향을 동일 확률(50%)로 선택.
- 특징: 균등 확률로 방향을 선택하므로, 부하 분산이 일부 이루어짐.
- Tornado traffic에서 throughput: 0.40
3. Weighted Random Routing- 방법: 짧은 방향을 높은 확률(1−d/8), 긴 방향을 낮은 확률(d/8)로 선택.
- 여기서 d는 source와 destination 간의 최소 거리.
- 특징: 트래픽을 짧은 경로에 집중하되, 일부는 긴 경로로 분산시켜 부하 분산 효과 향상.
- Tornado traffic에서 throughput: 0.53
4. Adaptive Routing- 방법: 현재 로컬 채널 부하를 고려하여 트래픽이 덜 혼잡한 방향으로 선택.
- 큐 길이나 과거의 패킷 수로 채널 부하를 추정.
- backtracking은 허용되지 않음 → source에서 한 번만 결정.
- 특징: 실시간 네트워크 상태를 반영하여 경로 결정.
- Tornado traffic에서 throughput: 0.53 (weighted random과 동일 수준)
- 방법: 목적지까지의 최단 거리 방향으로 항상 라우팅함.
최악의 경우 throughput을 가장 잘 보장하는 알고리즘은 무엇일까? 대부분의 사람들은 greedy 알고리즘을 선택한다. 실제로 2002년 박사 자격 시험에서 이 문제가 출제되었고, 응시자의 90% 이상이 greedy 알고리즘을 선택했다. 하지만 이 알고리즘은 최악의 경우에 최선의 throughput을 제공하지 않는다.
예를 들어, 각 노드 i가 i+3 mod 8로 패킷을 보내는 tornado traffic pattern을 보자. 이때 greedy routing을 사용하면 모든 트래픽이 ring을 시계방향으로만 이동하고, 반시계 방향 채널은 사용되지 않아 부하 불균형이 심해진다. 이로 인해 각 terminal의 throughput은 b/3으로 떨어진다. 반면, random routing에서는 반시계방향 링크에 5/2의 부하가 걸려 throughput은 2b/5가 된다. Weighted random은 전체 트래픽 중 5/8이 3 링크를, 3/8이 5 링크를 지나므로 부하는 각 방향에 대해 15/8이 되고, throughput은 8b/15가 된다. Adaptive routing도 잘 구현된다면 이와 같은 부하 균형을 달성하여 동일한 throughput을 낼 수 있다.
이 예시는 라우팅 선택이 부하 균형에 얼마나 큰 영향을 미치는지를 보여준다. 물론 throughput은 최적화할 수 있는 여러 지표 중 하나일 뿐이고, 어떤 지표를 중시하느냐에 따라 적절한 알고리즘 선택은 달라질 수 있다.


8.2 라우팅 알고리즘의 분류
라우팅 알고리즘은 source node x에서 destination node y까지 가능한 경로 집합 Rxy 중에서 어떻게 선택하는지를 기준으로 분류할 수 있다.
- Deterministic routing: 항상 동일한 경로를 선택한다 (Rxy의 크기가 1 이상이라도 항상 같은 경로 선택). topology의 경로 다양성을 무시하므로 부하 분산에는 매우 취약하다. 그럼에도 구현이 쉽고 deadlock-free로 만들기 쉬워서 널리 사용된다.
- Oblivious routing: deterministic 알고리즘을 포함하는 개념으로, 현재 네트워크의 상태를 전혀 고려하지 않고 경로를 선택한다. 예를 들어, 가능한 모든 경로에 대해 트래픽을 균등 분산하는 random 알고리즘이 이에 해당한다.
- Adaptive routing: 네트워크의 상태에 따라 동적으로 경로를 선택한다. 상태 정보는 노드나 링크의 사용 여부, 큐 길이, 채널 부하 이력 등을 포함할 수 있다.
앞서 소개한 tornado 예제는 이 세 가지 유형의 예시를 모두 포함한다. Ring에서 greedy는 deterministic routing, random과 weighted random은 oblivious routing, adaptive는 초기 hop의 채널 부하를 고려하므로 adaptive routing이다.
이때 언급된 알고리즘들은 Rxy, 즉 최소 경로 집합을 기준으로 한 것이며, 이를 minimal routing이라고 한다. 반면, minimal이 아닌 경로도 포함하는 경우 R′xy에서 선택하며 이를 non-minimal routing이라고 한다. Ring 예제에서 greedy는 minimal, random과 adaptive는 non-minimal로 분류된다.
8.3 라우팅 관계 (Routing Relation)
라우팅 알고리즘을 라우팅 관계 R과 선택 함수 ρ로 나누어 표현하면 유용하다. R은 경로(또는 incremental routing에서는 채널)들의 집합을 반환하고, ρ는 그 중 하나를 선택하는 역할을 한다.
라우팅 알고리즘이 incremental인지, node 기반인지 channel 기반인지에 따라 R은 세 가지 방식으로 정의된다.
- R: N × N → P(P)
두 노드 간 가능한 전체 경로의 집합을 반환한다. 이를 all-at-once routing이라 부른다. - R: N × N → P(C)
현재 노드와 목적지를 입력으로 받아 가능한 채널들의 집합을 반환한다. - R: C × N → P(C)
현재 채널과 목적지를 입력으로 받아 가능한 채널들의 집합을 반환한다.
첫 번째 방식은 라우팅 결정을 source에서 한 번에 수행하고 패킷과 함께 경로 정보를 저장한다. 계산은 단순하지만, 패킷마다 경로 정보를 함께 보내야 하므로 오버헤드가 있다.
두 번째, 세 번째 방식은 incremental routing으로, hop마다 라우팅 결정을 반복 수행한다. 패킷마다 경로 정보를 들고 다닐 필요는 없지만, hop마다 R을 계산해야 하므로 latency가 증가할 수 있다. 또한, 일부 라우팅 전략은 incremental 방식으로는 구현할 수 없다.
특히 Relation 8.2 방식은 수직에서 수평, 혹은 그 반대 방향으로 들어오는지를 구분하지 못하므로 2-D mesh에서 특정 노드에서만 방향 전환을 제한하는 전략은 구현 불가하다. Relation 8.3은 이를 어느 정도 해결할 수 있다. 이전 채널 정보를 활용해 deadlock 방지에도 효과적이다.
라우팅이 deterministic이 아니라면, R은 여러 경로/채널을 반환하므로, 선택 함수 ρ가 최종 선택을 담당한다. ρ가 네트워크 상태를 고려하지 않으면 oblivious, 고려하면 adaptive가 된다.
8.4 Deterministic Routing
가장 단순한 형태인 deterministic routing은 모든 source-destination 쌍에 대해 항상 같은 경로를 선택한다. 예: R: N × N → P. 이는 경로 다양성이 없기 때문에 부하 불균형을 유발한다. 어떤 트래픽 패턴에서는 모든 deterministic routing이 심한 부하 불균형을 일으킨다.
그럼에도 불구하고, 구현이 간단하고 비용이 낮아 과거 네트워크에서 널리 사용되었고, 지금도 irregular topology에서는 자주 쓰인다. 이는 randomized나 adaptive 라우팅을 설계하기 어렵기 때문이다.
대부분의 topology에서는 minimal deterministic routing function을 선택하는 것이 합리적이다. 최소한 경로 길이는 짧게 유지된다. 일부 topology에서는 간단한 deterministic 접근 방식이 adaptive를 포함한 다른 어떤 minimal routing algorithm보다도 부하 분산이 잘 되는 경우도 있다 (Exercise 9.2 참고). 또한 특정 source-destination 쌍 사이에서 메시지 순서를 유지해야 하는 경우, deterministic routing이 이를 단순하게 보장하는 방법이 될 수 있다. 이는 예를 들어 특정 cache coherence protocol에서 중요하다.
이 절에서는 가장 널리 쓰이는 deterministic routing algorithm 두 가지, 즉 butterfly에서의 destination-tag routing과 torus/mesh에서의 dimension-order routing을 설명한다.
8.4.1 Butterfly Network에서의 Destination-Tag Routing
k-ary n-fly network에서 (4.1절 참고) 목적지 주소는 radix-k 숫자 n자리로 해석되며, 이것이 경로 선택에 직접 사용된다. 주소의 각 자릿수는 네트워크 각 단계에서 출력 포트를 선택하는 데 사용된다. 이는 마치 source-routing table에서 미리 정해진 routing header처럼 동작한다. 2장에서 설명한 단순 router에서 사용된 방식이다.
Figure 8.3(a)는 source 3에서 destination 5까지 가는 경로를 예시로 보여준다. 5의 이진수는 101이고, 각 비트는 네트워크의 각 단계에서 출력 포트를 결정한다. 첫 번째 비트 1은 아래쪽 출력 포트를, 두 번째 비트 0은 위쪽 포트를, 세 번째 비트 1은 다시 아래쪽 포트를 선택한다.
이 예에서 출발 노드 3의 주소는 실제로 사용되지 않았다. 다시 말해, 어떤 노드에서 출발하더라도 101 패턴을 따라가면 목적지 5에 도달한다. 이는 모든 목적지 주소에 대해 동일하게 적용된다. 즉, destination-tag routing은 목적지 주소에만 의존하며 source와는 무관하다.
Figure 8.3(b)는 4-ary 2-fly network에서 7번 노드에서 11번 노드로 가는 경로를 보여준다. 여기서 목적지 주소 11은 234(4진수)로 해석되며, 첫 번째 router에서 포트 2(위에서 세 번째), 두 번째 router에서 포트 3(맨 아래)을 선택한다. 이 역시 출발 노드에 상관없이 목적지를 정확히 선택할 수 있다.

8.4.2 Cube Network에서의 Dimension-Order Routing
dimension-order 또는 e-cube routing은 torus 및 mesh와 같은 direct k-ary n-cube network에서 destination-tag routing과 유사한 방식이다. 목적지 주소를 radix-k 숫자로 해석하고, 각 자릿수를 하나씩 사용하여 경로를 결정한다. 하지만 butterfly network와 달리 cube network에서는 한 자릿수를 해결하기 위해 여러 hop이 필요할 수 있다.
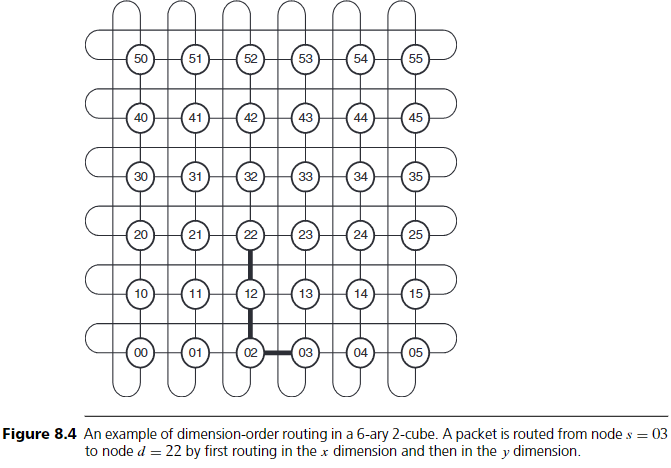
예를 들어 Figure 8.4의 6-ary 2-cube에서 node 03에서 node 22로 이동하는 패킷을 보자. torus에서는 각 차원을 시계방향 또는 반시계방향으로 이동할 수 있으므로, 먼저 각 차원에서의 최단 방향을 계산해야 한다.
source s = (0, 3), destination d = (2, 2)일 때:
- m = (2 − 0, 2 − 3) mod 6 = (2, 5)
- Δ = (2, 5) − (0, 6) = (2, -1)
- D = (+1, -1) → x 차원은 +1 방향(시계방향), y 차원은 -1 방향(반시계방향)
이 정보를 기반으로 패킷은 먼저 x 차원에서 이동하고, 목적지 좌표에 도달하면 y 차원으로 전환한다. Figure 8.4에서 node 03에서 시작하여 x 차원으로 한 hop(03 → 02), y 차원으로 두 hop(02 → 12 → 22) 이동한다.
목적지를 32로 변경하면 Δ = (3 − 0, 2 − 3) = (3, 5) → D = (0, -1). y 방향의 preferred direction이 0이 된다. 이는 양방향 모두 3 hop이 필요하다는 뜻이며, 이 경우 부하를 균형 있게 분산하기 위해 deterministic routing 대신 무작위로 양방향으로 패킷을 나누는 것이 효과적이다. Equation 8.4를 보면, preferred direction이 0이 되는 경우는 k가 짝수일 때만 발생한다.
mesh에서는 wraparound channel이 없으므로 방향 선택이 단순해진다:
- DM,i = +1 if di > si, -1 otherwise
Dimension-order routing은 부하 분산 성능은 좋지 않지만, 다음 두 가지 이유로 널리 사용된다:
- 구현이 매우 간단하다. 특히 각 차원별로 router를 분할하여 dimension-slicing이 가능하다.
- 각 차원 간의 채널 dependency에 cycle이 생기지 않도록 하여 deadlock 방지를 단순화한다. 다만, 차원 내에서는 여전히 deadlock이 발생할 수 있다 (14장 참고).
8.5 사례 연구: Cray T3D에서의 Dimension-Order Routing
Figure 8.5는 최대 2,048개의 DEC Alpha processing element를 3-D torus로 연결한 Cray T3D를 보여준다. T3D는 shared-memory multiprocessor이며, 각 PE는 로컬 메모리를 가지며 다른 PE의 메모리에도 접근 가능하다. 각 PE 쌍은 하나의 router를 공유하고, 이 router는 네트워크 인터페이스를 통해 연결된다.
T3D는 dimension-order routing을 사용하며, Figure 8.6에 보이듯 각 차원(x, y, z)을 위한 동일한 ECL gate array로 구현된 dimension-sliced router를 사용한다. 이는 J-Machine router(5.5절)와 유사한 구조이다. 이러한 분할은 dimension-order routing 덕분에 가능하다.
패킷이 network interface로부터 들어오면, x router가 이를 받아 x 좌표가 목적지인지 판단한다. 목적지에 도달하지 않았다면 +x 또는 −x 방향으로 전달하고, x 좌표가 일치하면 다음 y router로 넘긴다.
패킷은 +x 방향(xpOut 채널)을 따라 전달된다. 이후 각 x router에서는 현재 위치가 목적지의 x 좌표와 일치하는지 확인한다. 일치하면 y router로 전달하고, 그렇지 않으면 계속 +x 방향으로 이동한다.
Cray T3D의 각 router 채널은 300 MBytes/s의 대역폭을 가지며, 모듈 간 wire mat을 통해 연결된다. 각 채널은 16비트 data와 8비트 control 신호로 구성되어 있으며, 150 MHz에서 동작한다. 이는 원래 Alpha 21064 프로세서와 동일한 클럭이다. Wire mat은 torus topology를 구성하기 위해 보드 엣지 커넥터에 수작업으로 연결된 여러 개의 wire들을 엮은 구조로, 불규칙하게 짜인 직물처럼 보여서 'mat'이라고 불린다. 각 data/control 신호는 wire mat 내에서 differential ECL 신호로 twisted pair를 통해 전달된다.
그림 8.6은 T3D router가 x, y, z 세 개의 차원에 대해 동일한 ECL gate array 칩 세 개로 분할되어 구성됨을 보여준다.
Cray T3D에는 I/O 노드가 포함되어 있으며, 이들은 x 및 z 차원으로만 네트워크에 연결된다. 이로 인해 torus topology는 다소 불규칙해진다. 일반적으로 메시지는 x에서 시작해서 z에서 끝나므로 문제가 없어 보이지만, 메시지를 보내는 노드가 I/O 노드와 y 차원만 다를 경우 문제가 발생할 수 있다. 이를 해결하기 위해 해당 노드에는 두 개의 주소가 부여된다. 이 문제는 Exercise 8.8에서 더 자세히 다룬다.

8.6 참고 문헌
Tornado traffic 문제와 weighted random 해법은 Singh 외 [168]에서 설명되었다. 라우팅 관계의 여러 형태와 이들이 deadlock 분석에서 가지는 중요성은 Dally [57]와 Duato [60, 61, 62]에 의해 다루어졌다. Butterfly network에서의 destination-tag routing은 Lawrie [110]가 처음 설명했으며, torus network에서의 e-cube routing은 Sullivan과 Bashkow [179]가 제안했다. Degree δ를 가진 네트워크에 대해 Borodin과 Hopcroft [28], Kaklamanis 외 [91]는 특정 트래픽 패턴이 deterministic routing 알고리즘에서 최소 √(N/δ) 이상의 채널 부하를 유도할 수 있음을 보여주었다.
8.7 연습문제
8.1 Section 8.1의 라우팅 알고리즘과 네트워크를 다시 고려하라. 다음 조건에서 최적의 알고리즘은 무엇인가?
(a) 최소 메시지 지연
(b) 균일 트래픽에서 최고의 throughput
(c) 다양한 permutation 트래픽 패턴에서 평균 throughput 최대화
각 조건당 하나의 알고리즘만 선택하고 그 이유를 설명하라.
8.2 Incremental routing의 한계
관계식 8.1(path-based relation)으로는 표현할 수 있지만, 관계식 8.2 및 8.3(incremental form)으로는 표현할 수 없는 라우팅 알고리즘을 설명하라.
8.3 Incremental 및 all-at-once routing의 header bit
Destination-tag routing을 incremental 또는 all-at-once 방식으로 구현할 수 있다. 각 방식에 대해 패킷에 저장되어야 할 비트 수를 계산하라. 어느 방식이 비트 수가 적은가? 이 관계는 일반 topology의 minimal routing에서도 성립하는가? Topology의 path diversity와 어떤 관련이 있는가?
8.4 Ring에서 backtracking 허용
Section 8.1에서 다룬 라우팅 예에서 backtracking을 허용한다면, weighted random 알고리즘보다 더 나은 최악의 경우 throughput을 제공하는 알고리즘을 개발할 수 있는가? 있다면 제시하고, 없다면 그 이유를 설명하라.
8.5 Stage가 추가된 butterfly에서의 라우팅
k-ary n-fly에서 하나 이상의 stage가 추가된 구조를 위한 deterministic 방식의 destination-tag routing 확장 방법을 설명하라. 부하 분산을 개선하기 위한 간단한 randomization 방법도 제안하라.
8.6 Cray T3D에서의 방향-우선 라우팅
Figure 8.6의 Cray T3D router 채널 레이블을 재배열하여 첫 번째 router는 +x와 +y, 두 번째는 +z와 −x, 세 번째는 −y와 −z를 처리하게 만든다고 하자. 이 분할 방식에서도 동작 가능한 라우팅 알고리즘을 설명하라. 한 번 router에 도달한 패킷은 이전 router로 돌아갈 수 없음을 명심하라.
8.7 방향-우선 라우팅의 장점
Exercise 8.6에서 유도한 라우팅 알고리즘이 dimension-order routing보다 가지는 장점은 무엇인가?
8.8 T3D에서 I/O 노드 라우팅
T3D 네트워크에서 I/O 노드는 x 및 z 차원에만 추가된다. 예를 들어, (0,0,0)부터 (3,3,3)까지 주소를 갖는 64-node 4-ary 3-cube가 있다고 하자. 이때 (4,0,0) 또는 (0,0,4)와 같은 주소로 I/O 노드를 추가할 수 있다. 모든 내부 노드에서 I/O 노드로, 그리고 그 반대로 dimension-order routing으로 라우팅이 가능하도록 하기 위해 I/O 노드에 두 개의 주소를 어떻게 부여할 수 있는지 설명하라.
8.9 Torus에서 “정확히 반대 방향” 트래픽 부하 균형
Dimension-order routing에서는 torus에서 노드가 정확히 반대 방향에 있을 때 부하 균형 문제가 발생할 수 있다. 이때 항상 positive 방향만 선택한다면 균일 트래픽에서의 throughput은 어떻게 되는가? 최악의 경우 throughput은 얼마인가? capacity의 분수로 표현하라. deterministic 알고리즘을 유지하면서도 이러한 반대 방향 부하 균형 문제를 개선할 수 있는 방법을 제안하고, 균일 및 최악의 throughput을 다시 계산하라.
8.10 CCC에서의 minimal routing
Exercise 5.8에서 설명한 일반 CCC topology에 대해 near minimal routing 알고리즘을 설계하라. 항상 정확한 최소 경로를 찾기보다 단순함을 우선하되, 생성되는 경로가 [128]에서 보여준 최대 직경 Hmax = 2n + ⌈n/2⌉ − 2를 초과하지 않도록 하라. 균일 트래픽에서의 부하 분산 특성도 논의하라.
'System-on-Chip Design > NoC' 카테고리의 다른 글
| Adaptive Routing (1) | 2025.06.02 |
|---|---|
| Oblivious Routing (3) | 2025.06.02 |
| Slicing and Dicing (1) | 2025.06.02 |
| Non-Blocking Network (2) | 2025.06.02 |
| Torus Networks (2) | 2025.06.02 |
