지금까지는 packet-switched 네트워크에 초점을 맞추었지만, 이 장에서는 circuit-switched 네트워크로 관심을 전환한다. circuit-switched 네트워크에서는 특정 source와 destination 간의 연결을 먼저 설정한 다음, 데이터가 해당 연결을 통해 연속적으로 흐르도록 유지하고, 이후 연결을 해제한다.
역사적으로 non-blocking, circuit-switched 네트워크는 전화 시스템과 처음 연관되었다. 한 사람이 다른 사람에게 전화를 걸면 단일 연결 요청을 의미한다. 전화가 연결되기 위해서는 네트워크 내에서 사용되지 않은 경로를 찾아 해당 경로를 그 통화에 할당해야 했다. 만약 전화 시스템이 non-blocking이었다면, 수신자의 전화기가 사용 중이지만 않다면 항상 통화 연결이 성공했을 것이다.
좀 더 정확하게 말하면, 네트워크가 non-blocking이라는 것은 입력과 출력의 임의의 순열(permutation)에 대해 모든 회로 요청을 처리할 수 있다는 의미다. 즉, 각 입력에서 선택된 출력까지의 전용 경로가 충돌(shared channel) 없이 형성될 수 있다. 반대로, 네트워크가 blocking이라면 이러한 모든 회로 요청을 충돌 없이 처리할 수 없다.
이 장에서는 두 가지 유형의 non-blocking 네트워크를 살펴본다. 먼저, 네트워크가 strictly non-blocking이라는 것은 이미 설정된 회로들을 재배치(reroute 또는 rearrange)하지 않고도 순차적으로 회로를 하나씩 설정하여 어떤 permutation이든 구성할 수 있다는 의미다. 즉, 아직 사용되지 않은 입력을 아직 사용되지 않은 출력에 연결하더라도 기존 트래픽의 경로에 영향을 주지 않으면 strictly non-blocking이다.
반면, 네트워크가 rearrangeably non-blocking(또는 간단히 rearrangeable)이라는 것은 임의의 permutation에 대해 회로를 설정할 수는 있지만, 이후에 설정되는 회로들을 위해 먼저 설정된 회로들을 재배열해야 할 수도 있음을 의미한다. rearrangeable 네트워크는 어떤 미연결된 입력과 출력이라도 연결할 수 있지만, 그 연결을 위해 다른 트래픽을 우회시켜야 할 수 있다.
위 정의들은 모두 각 입력이 최대 한 개의 출력에만 연결되는 unicast 트래픽에 해당된다. 또한 한 입력이 여러 출력으로 퍼지는 multicast 트래픽도 고려한다. multicast 트래픽에 대해 네트워크가 strictly non-blocking이라는 것은 다른 트래픽에 영향을 주지 않고 어떤 미연결 출력이라도 어떤 입력(연결 여부 무관)과 연결할 수 있다는 의미다. 또한 rearrangeable한 multicast 네트워크는 어떤 미연결 출력이라도 어떤 입력과 연결할 수 있으나, 그 연결을 위해 다른 트래픽을 우회시켜야 할 수 있다.
Crossbar 스위치와 expansion이 2:1인 Clos 네트워크는 unicast 트래픽에 대해 strictly non-blocking 네트워크의 예시다. Crossbar 스위치와 더 큰 expansion을 가진 Clos 네트워크는 multicast 트래픽에 대해서도 strictly non-blocking하다. Beneš 네트워크와 expansion이 없는 Clos 네트워크는 unicast 트래픽에 대해 rearrangeable한 네트워크의 예시다.
6.1 Non-Blocking vs. Non-Interfering 네트워크
packet switching 응용에서는 non-blocking 네트워크의 개념은 대체로 무의미하거나 과도한 개념이다. packet switch는 연결 또는 세션 동안 회로를 고정하지 않기 때문에, 채널을 공유하더라도 두 가지 제약조건만 충족하면 간섭 없이 트래픽을 공유할 수 있다.
첫 번째는 채널 load γmax가 채널 대역폭보다 작아야 한다는 대역폭 제약이다. 두 번째는 buffer와 채널 대역폭 같은 자원을 할당할 때, 하나의 흐름이 다른 흐름의 서비스를 일정 시간 이상 방해하지 않도록 자원 할당이 이뤄져야 한다. 이러한 자원 할당 제약은 12장에서 설명하는 적절한 flow control 메커니즘을 통해 달성할 수 있다.
이러한 조건을 만족하는 packet-switched 네트워크를 non-interfering 네트워크라고 부른다. 이러한 네트워크는 임의의 packet 트래픽을 처리할 수 있으며, 패킷 지연에 대한 보장된 상한이 있다. 트래픽은 어떤 채널의 대역폭 용량도 초과하지 않으며, 흐름 간 자원 할당이 상호 간섭을 일으키지 않는다.
오늘날 대부분의 응용에서 사람들이 non-blocking 네트워크를 원한다고 말할 때, 실제로 필요한 것은 이런 non-interfering 네트워크이며, 이는 훨씬 적은 비용으로 실현할 수 있다. 그러나 역사적 이유와 진정한 non-blocking이 필요한 경우(예: 회로 전환을 지원해야 할 경우)를 위해, 이 장의 나머지 부분에서는 non-blocking 네트워크에 대해 간략히 살펴본다.
항목 non-blocking non-interfering
| 사용 환경 | circuit-switched | packet-switched |
| 연결 방식 | 회로 고정 | 자원 공유, time-multiplexing |
| 충돌 회피 방식 | 회로 수 늘리기 or 재배치 | flow control, buffer allocation |
| 목표 | 연결 요청 항상 수용 | 간섭 없이 지연·성능 보장 |
| Clos 적용 | Clos의 주 개념 | Clos는 구조만 쓰고 packet에도 적용 가능 |
6.2 Crossbar 네트워크
n × m crossbar 또는 crosspoint switch는 중간 단계 없이 n개의 입력을 m개의 출력에 직접 연결한다. 본질적으로 이러한 스위치는 m개의 n:1 multiplexer로 구성된다.
대부분의 crossbar 네트워크는 정사각형 형태(n = m)이지만, m > n 또는 m < n인 직사각형 형태도 있다.

그림 6.1은 4×5 crossbar의 개념적 모델을 보여준다. 입력선 4개와 출력선 5개가 있으며, 입력선과 출력선이 교차하는 지점마다 입력선을 출력선에 선택적으로 연결하는 switch, 즉 crosspoint가 존재한다. 올바른 동작을 위해서는 각 출력이 최대 하나의 입력과만 연결되어야 한다. 그러나 입력은 여러 출력에 연결될 수 있다. 예를 들어, 그림 6.1에서는 입력 1이 출력 0과 3에 연결되어 있다.
한때 전화망 대부분은 그림 6.1과 같은 구조의 기계 릴레이로 구성된 crossbar switch를 사용하여 구현되었다. 이런 switch 기반 crossbar에서는 입력과 출력의 구분이 실질적으로 없으며, switch가 만들어내는 연결은 양방향이다.
그러나 현재 대부분의 crossbar는 디지털 로직으로 구현되며, 그림 6.2와 같은 구조를 가진다. 각 입력선은 m개의 n:1 multiplexer 중 하나의 입력으로 연결되고, multiplexer의 출력이 m개의 출력 포트를 구동한다. 이 multiplexer는 tri-state gate나 wired-OR gate로 구성될 수 있으며, 그림 6.1의 구조를 모방하거나 전통적인 로직 게이트 트리로 구성될 수 있다.

crossbar switch를 시스템 내에 그릴 때마다 전체 회로도를 그리지 않기 위해, 그림 6.3과 같은 crossbar 기호를 사용한다. 문맥상 상자 모양이 crossbar switch임이 명확할 경우에는 'X' 기호를 생략하고 단순한 입력과 출력이 있는 박스로 나타낸다.

crossbar switch는 unicast와 multicast 트래픽 모두에 대해 명백히 strictly non-blocking이다. 연결되지 않은 어떤 출력이라도 입력과 연결하기 위해 단순히 해당 입력과 출력 사이의 switch를 닫거나 multiplexer 설정을 조정하면 되기 때문이다. 많은 다른 네트워크들이 이러한 속성을 얻기 위해 복잡한 노력을 해야 하지만, crossbar는 이 특성을 매우 쉽게 만족시킨다.
그렇다면 crossbar가 간단히 non-blocking 특성을 갖는다면 왜 다른 non-blocking 네트워크를 고민해야 할까? 그 이유는 비용과 확장성 때문이다. 작은 규모에서는 경제적이지만, n×n 정사각형 crossbar의 비용은 n²에 비례하여 증가한다. n이 커질수록, crossbar의 비용은 n log n에 비례하는 네트워크들에 비해 빠르게 증가하여 부담이 된다.
crossbar의 제곱 비용은 switch 자체의 구조와 여러 개의 작은 crossbar를 결합해 더 큰 crossbar를 구성할 때도 명확하게 드러난다. 그림 6.1과 6.2에서 볼 수 있듯이, 입력과 출력선의 그리드를 구성하는 데 n²의 면적이 필요하고, n²개의 crosspoint를 포함하기 위해 n²의 면적이 필요하며, n개의 multiplexer 각각이 n에 비례하는 면적을 차지하므로 총 n²의 면적이 요구된다.

그림 6.4에 보이듯이, 작은 crossbar를 사용해 큰 crossbar를 만들 때도 비용은 제곱적으로 증가한다. 2n×2n crossbar는 2×2 배열의 n×n crossbar 네 개로 구성할 수 있으며, 고속 신호를 지점 간으로 분배하기 위해 입력에 1:2 distributor가 필요하고, 출력에서는 2:1 multiplexer가 각 출력에 보낼 신호를 선택해야 한다. 일반적으로, jn×jn crossbar는 j×j 배열의 j²개의 n×n crossbar와 함께 n개의 1:j distributor 및 j:1 multiplexer로 구성할 수 있다.
현실적인 crossbar의 비용은 어떻게 패키징되는지에 따라 크게 달라진다. 시스템의 다른 구성 요소가 전혀 없는 단일 칩 안에 완전히 패키징된 crossbar는 pin 수(Wn)에 의해 크기가 제한되며, 칩에 crossbar를 구현하는 데 필요한 면적보다 pin 수가 더 중요한 제약이 된다. 이 경우 crossbar의 비용은 칩에 담을 수 있는 최대 크기까지는 선형적으로 증가한다. 그러나 crossbar가 칩에 들어가면서 다른 구성 요소들과 연결되어야 할 경우, 면적 제한이 중요해지며 이때는 제곱 비용이 문제가 된다. crossbar가 여러 칩에 걸쳐 구현되어야 할 경우(그림 6.4처럼), 크기에 따라 비용은 제곱적으로 증가한다.
6.3 Clos 네트워크
6.3.1 Clos 네트워크의 구조와 특성
Clos 네트워크는 세 개의 단계(stage)로 구성된 네트워크이며, 각 단계는 여러 개의 crossbar switch로 구성된다. 대칭 Clos 네트워크는 (m, n, r)의 세 개 숫자로 표현된다. 여기서 m은 중간 단계 switch의 수, n은 각 입력/출력 switch의 포트 수, r은 입력 및 출력 switch의 수를 의미한다.
Clos 네트워크에서 각 중간 단계 switch는 모든 입력 switch로부터 입력 링크를 하나씩 받고, 모든 출력 switch로 출력 링크를 하나씩 보낸다. 즉, r개의 입력 switch는 각각 n×m crossbar로, n개의 입력 포트를 m개의 중간 switch에 연결하며, m개의 중간 switch는 각각 r×r crossbar로, r개의 입력 switch를 r개의 출력 switch에 연결한다. 그리고 r개의 출력 switch는 각각 m×n crossbar로, m개의 중간 switch를 n개의 출력 포트에 연결한다. 예를 들어, (3,3,4) Clos 네트워크는 그림 6.5에, (5,3,4) Clos 네트워크는 그림 6.6에 나타나 있다. Clos 네트워크에서 입력과 출력 포트를 참조할 때는 switch 번호 s와 포트 번호 p를 사용해 s.p로 표기한다.
Clos 네트워크의 각 단계를 모두 연결하는 all-to-all 연결을 3차원 시각화로 표현하면(그림 6.7), 입력 및 출력 switch가 수평 방향으로 트래픽을 보내고 받고, 중간 switch는 수직 방향으로 트래픽을 전달하는 형태로 볼 수 있다. 이와 같은 교차 배열 구조는 소형 Clos 네트워크의 패키징에도 유용하며, 단계 간의 연결을 짧게 유지할 수 있게 한다.
(m, n, r) Clos 네트워크의 특성은 이 topology로부터 유도된다. Clos 네트워크는 세 단계로 구성되므로 hop 수 H = 4이다. 이 네트워크는 그림 6.7과 같이 수평 또는 수직으로 이등분할 수 있다. 중간 switch를 가로로 가르는 절단(bisection)의 경우 bisection bandwidth BC = mr이며, 입력과 출력 switch를 세로로 가르는 경우 BC = 2nr = 2N이다. 실제로는 대부분의 네트워크가 입력과 출력 switch를 함께 배치하고 switch 간의 모든 연결선을 절단한다.

그림 6.5
(m = 3, n = 3, r = 4)인 대칭 Clos 네트워크는 r = 4개의 n×m 입력 스위치, m = 3개의 r×r 중간 스위치, r = 4개의 m×n 출력 스위치로 구성된다. 모든 스위치는 crossbar이다.

그림 6.6
(5,3,4) Clos 네트워크. 이 네트워크는 unicast 트래픽에 대해 strictly non-blocking하다.
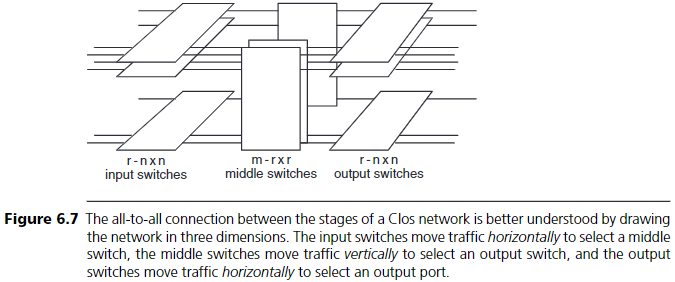
그림 6.7
Clos 네트워크의 각 단계 간 all-to-all 연결은 네트워크를 3차원으로 그리면 더 잘 이해할 수 있다. 입력 스위치는 수평 방향으로 트래픽을 이동시켜 중간 스위치를 선택하고, 중간 스위치는 수직 방향으로 트래픽을 이동시켜 출력 스위치를 선택하며, 출력 스위치는 다시 수평 방향으로 트래픽을 이동시켜 최종 출력 포트를 선택한다.
입력 및 출력 스위치의 degree는 δio = n + m이고, 중간 스위치의 degree는 δm = 2r이다.
Clos 네트워크의 가장 흥미로운 특성은 경로 다양성(path diversity)이며, 이 특성으로 인해 non-blocking 성질이 발생한다. m개의 중간 스위치를 가진 Clos 네트워크에서는 입력 a에서 출력 b까지 총 |Rab| = m개의 경로가 있으며, 각각은 서로 다른 중간 스위치를 경유한다.
Clos 네트워크에서 회로를 라우팅할 때 자유롭게 선택 가능한 유일한 지점은 입력 스위치이다. 여기서 사용 가능한 중간 스위치 중 하나를 선택할 수 있다. 중간 스위치는 출력 스위치로 가는 단일 링크만 선택해야 하며, 이 링크가 사용 중이면 해당 경로는 불가능하다. 마찬가지로 출력 스위치도 선택된 출력 포트를 선택해야 한다. 따라서 Clos 네트워크에서 라우팅 문제는 각 회로(또는 패킷)를 어느 중간 스위치에 할당할지를 결정하는 문제로 환원된다.
6.3.2 Unicast 라우팅 (Strictly Non-Blocking Clos 네트워크)
정리 6.1
Clos 네트워크는 m ≥ 2n − 1일 때, unicast 트래픽에 대해 strictly non-blocking이다.
증명
N − 1개의 통화가 설정되어 있고, 입력 a.i와 출력 b.j만 연결되지 않은 상황을 가정한다. 이전의 통화들은 입력 스위치 a와 출력 스위치 b에서 사용된 중간 스위치들이 서로 겹치지 않도록 설정되었다. 예를 들어, 스위치 a는 처음 n−1개의 중간 스위치를 사용하고, 스위치 b는 마지막 n−1개의 중간 스위치를 사용했다고 가정하자. a.i를 b.j에 연결하려면, a와 b 둘 다 사용하지 않은 중간 스위치가 최소한 하나는 존재해야 한다. 따라서 총 중간 스위치는 최소 2n − 1개가 필요하다.
예를 들어, 그림 6.6의 (5,3,4) Clos 네트워크는 m = 5 = 2n − 1 이므로 strictly non-blocking이다. 반면, 그림 6.5의 (3,3,4) 네트워크는 m = 3 < 5 이므로 strictly non-blocking하지 않다. 이 네트워크는 뒤의 6.3.3절에서 rearrangeable임을 보게 된다.
strictly non-blocking Clos 네트워크에서 unicast 통화를 라우팅하는 알고리즘은 그림 6.8과 같다. a.i에서 b.j로 unicast 통화를 라우팅할 때는, 입력 스위치 a와 출력 스위치 b가 사용하지 않은 중간 스위치들의 리스트를 교차하여 공통의 사용 가능한 중간 스위치를 선택하면 된다. 앞의 증명에서 본 바와 같이, 항상 최소 하나의 중간 스위치가 존재한다.
예를 들어, 입력 1.1 (1)에서 출력 3.3 (9)로 회선을 라우팅하는 경우를 보자 (그림 6.9). 입력 스위치 1은 이미 1.2 (2) → 4.1 (10) 및 1.3 (3) → 2.3 (6) 회선으로 인해 중간 스위치 1과 2 경로를 사용 중이다 (점선으로 표시). 한편, 출력 스위치 3도 3.1 (7)과 2.1 (4)에서 온 회선으로 인해 중간 스위치 4와 5 경로를 사용 중이다. 입력 및 출력 스위치는 각각 최대 n−1 = 2개의 중간 스위치만 차단할 수 있으므로, 최대 2n − 2 = 4개의 중간 스위치가 사용 중일 수 있다. m = 5 = 2n − 1이므로 항상 하나의 중간 스위치는 사용 가능하다. 이 경우, 중간 스위치 3이 사용 가능하여 굵은 선으로 나타난 경로를 통해 새로운 통화를 처리할 수 있다.
좀 더 포괄적인 라우팅 예제로, permutation {5, 7, 11, 6, 12, 1, 8, 10, 3, 2, 9, 4}를 고려하자. 즉, 입력 1 (1.1)은 출력 5 (2.2)로, 입력 2 (1.2)는 출력 7 (3.1)로, 등등으로 매핑된다. 이를 단순화하면 switch 단위 permutation {(2, 3, 4), (2, 4, 1), (3, 4, 1), (1, 3, 2)}가 된다. 중간 스위치 할당을 결정할 때는 switch만 고려하면 되고, 중간 스위치가 결정되면 입력과 출력 switch의 crossbar 설정은 non-blocking이므로 간단히 처리된다.
통화는 {9,6,7,8,3,12,10,5,1,11,2,4} 순서로 처리된다고 하자. 첫 번째 통화는 입력 9 (3.3)에서 출력 3 (1.3)으로 연결되고, 그 다음은 6 (2.2) → 1 (4.3) 순으로 진행된다.
그림 6.8
strictly non-blocking Clos 네트워크에서 unicast 통화를 라우팅하는 알고리즘:
For each call (a,b)
freeab = free(a) ∧ free(b) // a와 b 모두에서 사용 가능한 middle switch 목록
middle = select(freeab) // 그 중 하나 선택
assign((a,b), middle) // 라우팅 설정※ 이 증명 기법은 비둘기집 원리(pigeonhole principle)로, 다양한 스케줄링 문제에 유용하게 사용된다.
그림 6.9
(5,3,4) Clos 네트워크에서 입력 1.1 → 출력 3.3으로 라우팅. 입력 스위치 1은 중간 스위치 1과 2로의 경로가 이미 점유되어 있으며, 출력 스위치 3은 중간 스위치 4와 5로의 경로가 점유되어 있다. 유일하게 사용 가능한 경로는 중간 스위치 3을 경유하는 경로이며, 이는 굵은 선으로 표시된다.

표 6.1
Strictly non-blocking Clos 네트워크에서 call set {(2, 3, 4), (2, 4, 1), (3, 4, 1), (1, 3, 2)}를 {9,6,7,8,3,12,10,5,1,11,2,4} 순서로 라우팅한 예이다. 각 행은 하나의 call 설정을 나타낸다. 열에는 입력(In), 출력(Out), 중간 스위치(Middle), 그리고 각 입력 및 출력 스위치의 free 벡터가 표시되어 있다.

이러한 bit-vector 표현을 이용하면, 입력 스위치 a에서 출력 스위치 b로 새로운 call을 설정할 때 다음과 같이 처리한다. 입력 스위치 a의 free 벡터와 출력 스위치 b의 free 벡터를 AND 연산하여, 두 스위치에서 모두 사용 가능한 중간 스위치를 나타내는 벡터를 얻는다. 각 free 벡터는 최대 두 개의 0을 가질 수 있으므로, AND 결과에는 최대 4개의 0만 있고, 최소 하나의 1이 반드시 존재한다. 이 1 중 하나를 선택하여 새로운 call에 사용할 중간 스위치를 결정한다.
예를 들어, 표 6.1의 마지막 call은 입력 4 (2.1) → 출력 4 (2.1)로 연결된다. 이 call 이전에 입력 스위치 2의 free 벡터는 10101 (2번, 4번 중간 스위치 사용 중), 출력 스위치 2의 free 벡터는 00111 (1번, 2번 중간 스위치 사용 중)이었다. 이를 AND 연산하면 00101이 되어 중간 스위치 3과 5가 사용 가능함을 나타낸다. 여기서 중간 스위치 3이 선택된다.
Strictly non-blocking Clos 네트워크의 라우팅 절차는 매우 단순하다. 그러나 이 단순함에는 비용이 따른다. strictly non-blocking 네트워크는 해당 rearrangeable 네트워크보다 거의 두 배의 비용이 들며, 중간 스위치를 2n−1/n배 더 많이 필요로 한다. 따라서 대부분의 응용에서는 rearrangeable 네트워크가 선호된다.
6.3.3 Rearrangeable Clos 네트워크에서의 Unicast 라우팅
정리 6.2
m ≥ n인 Clos 네트워크는 rearrangeable하다.
Clos 네트워크 라우팅에 대한 이해를 돕기 위해, 회선 집합을 **이분 그래프(bipartite graph)**로 표현한다. 입력 스위치 집합과 출력 스위치 집합이 각기 그래프의 정점 집합을 이루며, 각 call은 그 사이의 간선으로 표현된다. 이때 라우팅 문제는 간선 색칠(edge coloring) 문제로 바뀐다. 각 중간 스위치가 하나의 색으로 간주되며, 동일한 정점에 같은 색이 두 번 이상 연결되지 않도록 각 간선에 색을 할당해야 한다. (즉, 하나의 입력 또는 출력 스위치에서 중간 스위치를 중복 사용하지 않아야 한다.)
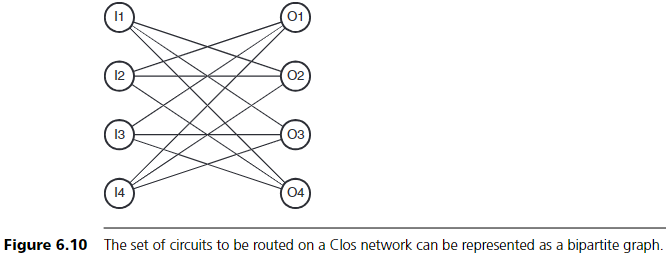
예를 들어 Section 6.3.2에서의 회선 집합 {(2,3,4), (2,4,1), (3,4,1), (1,3,2)}를 생각해 보자. 입력 스위치 1은 출력 스위치 2,3,4에 연결되고, 스위치 2는 2,4,1에, 스위치 3은 4,1에, 스위치 4는 3에 연결된다. 이 call 집합을 표현하는 이분 그래프는 그림 6.10과 같다.

그림 6.11에는 rearrangeable non-blocking 네트워크에서 call 집합을 라우팅하는 알고리즘이 제시되어 있다. 이 알고리즘은 입력 스위치 a에서 출력 스위치 b로 call을 라우팅할 때, 우선 a와 b 모두에서 사용 가능한 중간 스위치가 있는지 확인한다. 존재하면 해당 스위치를 선택하여 바로 라우팅한다. 이 과정은 Figure 6.8에 나온 strictly non-blocking 라우팅 절차와 동일하다.
공통의 free 중간 스위치가 없다면, 다음과 같은 절차가 반복적으로 실행된다:
- 입력 스위치 a에서 사용 가능한 중간 스위치 mida를 선택한다.
- 출력 스위치 b에서 해당 mida를 사용하는 call (c,b)이 있다면,
- 그 call을 midb (출력 b에서 사용 가능한 다른 중간 스위치)로 옮긴다.
- 만약 midb가 이미 입력 c에서 사용 중이라면, 이 과정을 반복하면서 call (c,d)를 (a,b)로 바꾸어 재귀적으로 이동시킨다.
이 알고리즘의 적용은 Table 6.2에 나타나 있으며, Section 6.3.2에서의 call 순서에 따른 라우팅 결과를 보여준다. 첫 번째로 재배치가 필요한 시점은 8번째 row에서 입력 2 → 출력 4인 call (2,4)를 설정할 때이다. 이 상황은 그림 6.12(a)에 나타나 있으며, 알고리즘은 다음과 같이 작동한다:
- (2,4)는 스위치 mida = 1을 사용해 라우팅을 시도한다.
- 하지만 출력 스위치 4는 이미 1번과 3번 중간 스위치를 사용 중이다.
- 따라서 (1,4) call을 midb = 2로 옮기고, (2,4)는 mida = 1로 설정된다. 그림 6.12(b) 참조.
더 복잡한 rearrangement는 11번째 row에서 (4,3) call을 설정할 때 발생한다. 이 시점은 그림 6.13(a)에 나타나 있으며, 중간 스위치 충돌로 인해 여러 call들이 연쇄적으로 재배치된다. 이 chain은 다음과 같다: (I3,O3), (I3,O1), (I2,O1), (I2,O4), (I1,O4). 각 call은 mida와 midb를 교대로 사용하면서 반복적으로 위치를 바꾼다. 그림 6.13(d)는 모든 재배치가 끝난 후의 상태를 보여준다.
표 6.2
call 집합을 rearrangeable Clos 네트워크에 라우팅한 결과. 열에는 새로 설정된 call, 이전 call, 중간 스위치(Middle), 각 입력 및 출력 스위치의 free 벡터가 포함된다.

정리 6.3
Looping 알고리즘으로 하나의 call을 설정할 때, 최대 2r − 2개의 다른 call을 재배치하게 된다.
증명
이 알고리즘은 이분 그래프 내 동일 정점을 두 번 방문하지 않기 때문에, 최대 2r개의 정점을 방문한 후 반복을 종료한다. 세 번째 정점부터 call 재배치가 시작되므로, 최대 2r − 2개의 call이 재배치된다.
이 알고리즘의 경로가 **비순환(acyclic)**임을 확인하기 위해 그림 6.14에서 conflict chain을 펼쳐본다. a₁, b₁은 첫 iteration의 입력 및 출력 스위치를 나타내며, 이후 iteration에서는 호출을 mida와 midb 사이로 반복적으로 이동시킨다.

그림 6.12
Figure 6.10의 call set을 라우팅하는 각 단계를 보여준다. 중간 스테이지에 대한 할당은 간선의 점선으로 표시된다.
(a) (I2, O4)를 라우팅하기 전에는 I2와 O4 모두에서 사용 가능한 중간 스위치가 없다.
(b) (I1, O4)를 중간 스위치 2로 이동시키면, (I2, O4)는 중간 스위치 1을 사용하여 라우팅할 수 있게 된다.
이제 어떤 정점도 다시 방문되지 않는다는 것을 귀납법으로 증명할 수 있다. a₁과 b₁은 각각 입력과 출력 스위치이므로 서로 다르다. i < j일 때 정점 aᵢ와 bᵢ가 서로 다르다고 가정하면, j번째에 방문하는 정점 aⱼ도 이전과 다르다. 이는 bj−1에서 mida 링크를 따라 찾았고, 이 mida는 a₁부터 aⱼ₋₁까지에서 이미 사용되었기 때문이다. 비슷하게 bj는 aj에서 midb 링크를 따라 찾은 것이므로 역시 이전과 겹치지 않는다. 따라서 어떤 정점도 중복 방문하지 않으며, 전체 정점 수가 2r이므로 알고리즘은 최대 2r번의 방문 후 종료되며 최대 2r−2개의 call만 재배치된다. (a₂, b₁)부터 시작하여 rearrangement가 일어난다.
정리 6.2 증명
알고리즘이 rn개의 call을 성공적으로 라우팅하고 종료되었으므로, m ≥ n인 Clos 네트워크는 임의의 unicast 트래픽에 대해 rearrangeable함이 증명된다.
call (a, b)를 설정하기 위해 기존 call (c, d)를 재배치해야 할 경우, 트래픽 손실 없이 call (c, d)를 새로운 경로로 전환하는 것이 바람직하다. 이러한 **무손실 전환(hitless switching)**은 입력, 중간, 출력 스위치를 동기화하여 call (c, d)의 i번째 단위(unit)는 이전 경로로, i+1번째 단위는 새 경로로 전송하도록 하면 실현할 수 있다. 이 단위는 bit, byte, frame 등일 수 있으며, 중요한 것은 전환의 정밀도가 아니라 동기화 여부다.
앞선 예제들은 이분 그래프에서 하나의 노드 쌍 사이에 하나의 간선만 존재하는 경우만 다루었으나, **중복 간선(multigraph)**도 고려해야 한다. 예를 들어, 입력 1.1에서 출력 3.3으로 가는 회로와 입력 1.2에서 출력 3.1로 가는 회로가 동시에 존재한다면, 스위치 관점에서는 I1에서 O3로 가는 두 개의 회선이 존재하게 된다. 이는 I1과 O3 사이에 두 개의 간선이 있는 multigraph가 된다. 다행히도 이러한 복잡성은 알고리즘의 성능에 영향을 주지 않으며, looping 알고리즘은 multigraph에도 잘 작동한다.
6.3.4 행렬 분해를 이용한 Clos 네트워크 라우팅
Rearrangeable Clos 네트워크는 **행렬 분해(matrix decomposition)**를 통해 라우팅할 수도 있다. 라우팅할 call 집합은 입력 스위치 i에서 출력 스위치 j로 가는 call의 수를 xᵢⱼ로 나타낸 요청 행렬 R로 표현된다. 예를 들어 다음과 같은 행렬이 있다고 하자:
이 요청 행렬은 각 행과 열의 합이 1 이하인 양의 행렬들의 합으로 분해될 수 있으며, 각 행렬은 중간 스위치의 하나의 설정에 대응된다. 예컨대 Table 6.2의 라우팅 결과는 다음과 같은 행렬 분해에 해당한다:
여기서 M₁, M₂, M₃는 permutation matrix로, Figure 6.5의 세 중간 스위치 설정에 대응된다. 앞서 언급했듯이, 하나의 입력-출력 스위치 쌍 사이에 여러 회로 요청이 있는 경우도 있으며, 이는 요청 행렬의 원소가 1보다 클 수 있음을 의미한다.
행렬 분해는 unicast, multicast 모두에 사용할 수 있으며, rearrangeable 또는 strictly non-blocking Clos 네트워크 모두에 적용할 수 있다. 구체적인 분해 알고리즘 유도는 독자 연습 문제로 남겨둔다.
6.3.5 Clos 네트워크에서의 Multicast 라우팅
Multicast call 집합 C = {c₁, ..., cₙ}에서 각 multicast call cᵢ = (aᵢ, {bᵢ₁, ..., bᵢf})는 입력 포트 aᵢ에서 f개의 출력 포트로의 연결을 의미한다. 여기서 fanout f는 연결된 출력 포트의 개수다. 각 입력 포트 및 출력 포트는 최대 하나의 call에만 포함되어야 한다. 다시 말해, 스위치 기준으로 표현할 경우 각 입력 및 출력 스위치는 최대 n개의 call에만 포함될 수 있다.
Clos 네트워크에서의 multicast 트래픽 라우팅은 unicast에 비해 더 어렵다. 그 이유는 다음 세 가지다:
- 더 많은 중간 스위치 필요: 최대 fanout이 f인 multicast call 집합을 라우팅하려면, 식 (6.5)에서 정의된 m(f)개의 중간 스위치가 필요하다.
- Looping 알고리즘이 적용 불가: fanout이 입력 스위치에서만 발생하는 경우가 아니라면, 중간 스위치에서의 fanout은 conflict graph에 cycle을 유발하여 알고리즘이 실패한다.
- fanout 위치 선택의 자유도: call이 fanout을 어디서 할지 — 입력 스위치, 중간 스위치, 또는 그 조합 — 를 선택할 수 있다. 이 추가적인 자유도를 잘 활용하는 것이 Clos 네트워크에서 multicast를 효율적으로 라우팅하는 핵심이다.
예를 들어, n = 3, r = 4인 Clos 네트워크에서 다음과 같은 fanout-2 call 집합을 라우팅한다고 하자:
C = {
(1, {1, 2}),
(1, {3, 4}),
(1, {1, 3}),
(2, {1, 4}),
(2, {2, 4}),
(2, {2, 3})
}
여기서도 회선은 포트가 아닌 스위치 번호로만 표현한다.
표 6.3은 이 call 집합의 conflict 벡터 표현을 나타낸다. 이 표는 각 입력 스위치와 출력 스위치에 해당하는 열을 가지며, 행 i는 call cᵢ = (aᵢ, {bᵢ₁, bᵢ₂})에 대해, aᵢ와 bᵢ₁, bᵢ₂ 위치에 1을 표시한다.
표 6.3의 첫 번째 행은 입력 스위치 1과 출력 스위치 1, 2 열에 1이 있는 것으로, call (1, {1, 2})를 나타낸다.
두 call cᵢ와 cⱼ는 그들의 벡터가 같은 열에 1을 공유하지 않을 때만 같은 middle switch를 공유할 수 있다. 다시 말해, cᵢ ∧ cⱼ = 0일 때만 동일한 중간 스테이지에 배치할 수 있다. 표 6.3을 보면, 모든 행 쌍이 non-zero 교집합을 가지므로, 입력 스위치에서 fanout을 수행하지 않는다면 이 여섯 개의 call을 라우팅하기 위해서는 여섯 개의 중간 스테이지 스위치가 필요하다.
입력 스위치에서 fanout을 수행하면, 출력 집합을 여러 middle stage로 분산할 수 있다. k-way 입력 fanout은 call cᵢ = (a, B)를 다음처럼 분할한다:
ci₁ = (a, B₁), ..., ciₖ = (a, Bₖ) 단, B₁ ∪ ... ∪ Bₖ = B 이고 각 Bⱼ는 서로 disjoint.
예를 들어, 표 6.3의 call 집합에서 c₃와 c₆에 대해 입력 fanout을 적용한 결과가 표 6.4에 나타나 있다. 이처럼 call을 분할하면 많은 pairwise conflict가 제거되고, 이 call 집합은 네 개의 middle-stage switch만으로도 라우팅할 수 있다 (표 6.5 및 그림 6.15 참조).
표 6.4
c₃와 c₆에 입력 fanout을 적용한 결과. 이 분할된 call 집합은 여섯 개가 아닌 네 개의 중간 스위치로 라우팅 가능.
표 6.5
표 6.4의 call 집합을 네 개의 middle switch에 배치한 결과.
그림 6.15
표 6.5에 따라 라우팅된 예시. c₃와 c₆의 fanout은 각각 입력 스위치 1과 2에서 수행되며, 나머지는 중간 스위치에서 fanout된다. 총 6개의 dual-cast call이 네 개의 middle stage switch에 라우팅되었다.
middle switch가 m개일 때, speedup은 S = m / n 이다. 일반적인 multicast call set을 라우팅하려면, 입력 스테이지에서 fanout을 S만큼 수행할 수 있다. 그러면 최대 fanout f는 중간 스테이지에서 g = ⌈f / S⌉ 만큼 수행해야 한다.
이때, 분할된 call은 벡터상 입력 스위치 1개와 출력 스위치 g개에 1이 존재하므로 총 g+1개의 열에서 1을 가진다. 각각의 열에는 최대 (n−1)개의 다른 call과 충돌할 수 있으므로, 하나의 call은 최대 (g+1)(n−1)개의 call과 충돌 가능하다. 따라서 다음 조건이 충족되면 모든 call은 충돌 없이 라우팅될 수 있다:
m ≥ (g + 1)(n − 1) + 1 (식 6.2)
f가 S로 나누어 떨어질 경우 다음과 같이 정리할 수 있다:
S = f / g ≥ ((g + 1)(n − 1) + 1) / n (식 6.3)
call을 입력 스테이지에서 분할한 후, 입력 열(column)은 최대 Sn개의 1을 가질 수 있지만, 하나의 call은 해당 열에서 최대 n개 call과만 충돌할 수 있다. 이는 동일한 main call에서 유도된 sub-call들끼리는 충돌하지 않기 때문이다.
표 6.6
중간 스위치 수에 따른 최대 fanout 값.
식 6.3에 따라, middle switch 수 m이 주어졌을 때, 지원 가능한 최대 fanout은 다음과 같다:
f ≤ m(m − n) / (n(n − 1)) (식 6.4)
표 6.6은 다양한 n과 S 값에 대해 처리 가능한 최대 fanout 값을 보여준다. 특히, n이 커질수록 (n−1 항 때문에) 같은 speedup에서도 지원 가능한 fanout이 급격히 감소함을 알 수 있다. 예: S = 2일 때 n=2면 f=4이나, n=48일 경우 f는 2.0 수준으로 감소한다.
식 6.4를 m에 대해 정리하면 다음과 같은 중간 스위치 수의 하한을 구할 수 있다:
m ≥ n + √(n² + 4n(n − 1)f)/2 = n + √((4f + 1)n² − 4fn)/2 (식 6.5)
단, 이 계산은 g가 정수일 때만 유효하며, 그렇지 않은 경우에는 **g = ⌈f / S⌉**로 올림해야 한다.
그림 6.16
Clos 네트워크에서 multicast call을 라우팅하는 greedy 알고리즘.
- call 집합 C에서 각 call을 분할하여, fanout이 최대 g가 되도록 Cs에 저장한다.
- 각 call cᵢ ∈ Cs에 대해
- 각 middle switch mⱼ에 대해
- 충돌이 없는 경우 mⱼ에 할당하고 다음 call로 진행.
- 각 middle switch mⱼ에 대해
**할당 행렬 A (m×2r 크기)**를 사용해 충돌 여부를 확인한다. 각 행은 middle switch에 해당하며, 열은 입력 또는 출력 스위치에 해당한다. A의 원소는 φ 또는 ck의 부모 call p(ck) 중 하나다. ck가 할당되면 관련 A의 항목들을 p(ck)로 채운다. 새로운 call ci = (ai, {bi₁,...,big})를 체크할 때, ai 및 biₖ들에 대한 A 항목이 모두 φ이거나 동일한 부모 p(cj)일 경우에만 충돌이 없는 것으로 판단한다.
정리 6.4
Greedy 알고리즘은 식 6.2에서 주어진 middle switch 수의 조건을 만족하며 multicast 트래픽을 라우팅할 수 있다.
증명
Cs 내에 어떤 call이 m개의 middle switch 모두와 충돌한다고 가정해 보자. 이는 해당 call이 m개의 call과 충돌해야 함을 의미한다. 하지만 한 call이 충돌할 수 있는 call 수는 (g+1)(n−1)를 초과할 수 없으므로, **m > (g+1)(n−1)**이면 반드시 하나의 switch가 남아 있다. 따라서 모순이다.
정리 6.5
(m, n, r) Clos 네트워크는 fanout이 f인 multicast 트래픽에 대해, 식 6.4가 성립하면 strictly non-blocking하다.
6.3.6 세 단계 이상의 Clos 네트워크
n×n crossbar switch를 구성 요소로 사용하면, n² 포트를 가진 rearrangeable한 (n, n, n) 3단계 Clos 네트워크를 만들 수 있다. 만약 n² 포트보다 더 많은 포트가 필요하다면, 이 n²×n² Clos 네트워크를 각 중간 스위치로 사용하고, 입력 및 출력 스위치는 n×n crossbar로 구성하면 된다. 이는 n³ 포트를 가진 5단계 Clos 네트워크를 형성하게 된다.
일반적으로, 정수 i에 대해, 다음과 같은 구조를 만들 수 있다:
- 첫 단계: nⁱ 개의 n×n crossbar
- 중간 단계: n개의 (2i−1)-단계 Clos 네트워크
- 마지막 단계: nⁱ 개의 n×n crossbar
이 구조는 총 2i+1단계로 구성되며, nⁱ⁺¹개의 포트를 가진 rearrangeable Clos 네트워크가 된다.
비슷한 방식으로, strictly non-blocking Clos 네트워크도 만들 수 있다. 이 경우에는 입력단에 expansion이 추가되어야 하며, 중간 스위치는 (2n−1)개의 nⁱ 포트를 갖는 (2i−1)단계 Clos 네트워크로 구성된다.
예를 들어, Figure 6.17은 (2,2,4) Clos 네트워크로, 이 네트워크는 2×2 crossbar로 구성되어 있으며, 중간 스테이지는 각각 (2,2,2) Clos 네트워크다.
5단계 Clos 네트워크에서의 라우팅은 Figure 6.11 또는 6.16의 알고리즘을 바탕으로 바깥에서 안쪽으로 진행된다. 각 call을 n개의 middle switch 중 하나에 할당함으로써, 하나의 (2i+1)-단계 스케줄링 문제를 n개의 (2i−1)-단계 문제로 분할한다. 이 과정을 i번 반복하여 최종적으로 ni개의 n×n crossbar 스케줄링으로 귀결된다.
예를 들어, i = 2인 5단계 Clos 네트워크에서 unicast call을 스케줄링할 경우:
- 첫 단계: call을 n개의 중간 스위치에 할당 (Figure 6.11 사용)
- 다음 단계: 각 중간 Clos 네트워크 (3단계)를 Figure 6.11로 처리
- 각 call은 중간 Clos 내의 하나의 crossbar로 다시 배정된다
Figure 6.17의 네트워크는 rearrangeably non-blocking 하며, 외부의 (2,2,4) Clos 네트워크도, 내부의 (2,2,2) 네트워크도 모두 rearrangeable하다.
반면, 동일한 구조에서 strictly non-blocking 성질을 만족하려면 각 입력 단계마다 expansion이 필요하다. 예: Figure 6.17과 같은 네트워크를 strictly non-blocking으로 만들려면 (3,2,4) Clos가 필요하며, 여기엔 다음이 포함된다:
- 입력: 네 개의 2×3 스위치
- 출력: 네 개의 3×2 스위치
- 중간: 세 개의 (3,2,2) Clos 네트워크 (각각은 2×3 입력, 3×2 출력, 2×2 middle switch 3개)
Strictly non-blocking 구조는 가운데 단계에 2×2 스위치가 9개 필요하며, 이는 rearrangeable 구조의 4개보다 많다. Expansion이 입력 및 중간 단계 양쪽 모두에서 요구되기 때문이다.
Multicast 라우팅을 위해서는 fanout을 어디에서 수행할지 결정해야 한다. 이 fanout은 네트워크의 어느 단계에서든 수행 가능하지만, 세부 사항은 이 책의 범위를 넘는다. 일반적인 휴리스틱은 2n+1단계 Clos 네트워크에서 fanout f를 각 첫 n+1단계마다 f^(1/(n+1))씩 분배하는 것이다.
6.4 Beneš 네트워크
Figure 6.17처럼 2×2 switch로만 구성된 Clos 네트워크는 Beneš 네트워크라고 불린다. 이 네트워크는 N = 2ⁱ 포트를 rearrangeable하게 연결할 수 있는 최소 crosspoint 수를 가진 네트워크이다.
N = 2ⁱ 포트를 2×2 스위치로 연결하려면, 2ⁱ−1단계가 필요하며, 각 단계마다 2ⁱ⁻¹개의 2×2 스위치가 필요하다. 총 스위치 수는 (2ⁱ−1)×2ⁱ⁻¹ = (2ⁱ−1)2ⁱ⁻¹이고, 각 스위치에 crosspoint 4개가 있으므로 총 crosspoint 수는 (2ⁱ−1)×2ⁱ⁺¹이다.
주의 깊은 독자라면, Beneš 네트워크는 두 개의 2-ary i-fly 네트워크를 중간에서 결합(fuse)한 구조와 동일함을 눈치챘을 것이다. 실제로는 Beneš 및 다른 다단 Clos 네트워크는 **중간 스테이지를 기준으로 folding(접기)**하여 구현되는 경우가 많다. 이때 스테이지 j와 2i−j는 동일한 패키지에 배치되어 배선 복잡도를 줄일 수 있다.
6.5 Sorting 네트워크
Sorting network는 N개의 입력에 unique key가 부착된 레코드를 받아, 정렬된 순서로 N개의 출력으로 내보낸다. Sorting network는 각 레코드의 목적지 주소를 정렬 key로 사용함으로써 non-blocking 네트워크로 사용할 수 있다.
Figure 6.18은 Batcher bitonic sorting network를 보여준다. 이 정렬 알고리즘은 bitonic sequence의 특성을 이용한다. Bitonic sequence는 순환적으로 봤을 때 최대 한 번씩 오름차순과 내림차순 구간만을 가지는 시퀀스이다.
예를 들어 Figure 6.18(a)에서는 8개의 key가 왼쪽에서 입력되고, 오른쪽에서 정렬된 결과로 출력된다. 각 화살표는 두 개의 key를 비교하여 필요한 경우 서로 교환한다. 첫 단계에서는 짝수/홀수 index별로 방향을 다르게 정렬하여 0–3번, 4–7번 구간이 각각 bitonic sequence가 되도록 만든다. 이후 단계에서는 각 bitonic 시퀀스를 monotonic sequence로 합친다.
총 6단계 후, 정렬이 완료된다. Table 6.7은 숫자 8개로 된 시퀀스에 bitonic 정렬을 적용한 예시를 보여준다.
N = 2ⁿ일 때, bitonic sort는 다음과 같은 단계 수를 갖는다:
S(N) = (log₂ N)(1 + log₂ N) / 2
즉, 2ⁿ의 길이를 갖는 bitonic 시퀀스를 만들기 위해 S(N/2) 단계, 그 후 정렬을 위해 log₂ N 단계가 필요하다.
Figure 6.18(b)의 sorting network는 이 알고리즘을 직접 하드웨어로 구현한 형태이며, 각 비교 연산은 key를 비교하여 라우팅하는 2×2 스위치로 구성된다.
6.6 사례 연구: Velio VC2002 (Zeus) Grooming Switch
일부 ATM 스위치에서는 Batcher 정렬 네트워크와 butterfly를 조합한 구조(Batcher-banyan 네트워크)를 사용한다. Batcher 네트워크는 입력 셀들을 목적지 주소로 정렬한다. 정렬된 출력에서는 trap stage가 동일한 출력을 가지는 셀을 감지하고 하나를 제외한 나머지를 제거한다. 남은 셀들은 서로 다른 출력을 가지며, 정렬된 상태로 butterfly 네트워크에 입력된다. 이 구조는 butterfly가 셀들을 충돌 없이 라우팅할 수 있게 한다.
Velio VC2002는 단일 칩으로 구현된 TDM(Time-Domain Multiplexing) 회로 스위치이다 (그림 6.19). VC2002는 총 72개의 SONET STS-48 2.488Gbps 직렬 입력 스트림을 받아, 동일한 수의 출력 스트림으로 출력한다. 각 STS-48 스트림은 48개의 STS-1 스트림(각 51.83Mbps)을 byte 단위로 멀티플렉싱하여 포함한다.
즉, 각 3.2ns의 byte time 또는 time slot마다 서로 다른 STS-1의 byte가 하나씩 전달된다. channel 0의 byte, channel 1의 byte, ..., channel 47의 byte 순으로 전송되고, 48개의 time slot 이후 동일한 패턴이 반복된다.
TDM switch, 또는 cross connect 혹은 grooming switch라 불리는 장치는 시간과 공간 두 차원에서 스위칭을 수행하여, 입력 STS-1의 time slot을 출력 STS-1의 time slot에 매핑한다.
그림 6.20은 입력 2개, 출력 2개, time slot 4개로 구성된 단순화된 TDM 스위칭 예시를 보여준다. 예를 들어 입력 0의 time slot 1에 있는 B는 출력 1의 time slot 0으로 라우팅된다 (unicast). 반면, 입력 0의 time slot 0에 있는 A는 출력 0의 time slot 3과 출력 1의 time slot 1로 동시에 전송된다 (multicast).
VC2002는 이와 유사한 기능을 72개의 입력과 48개의 time slot에 대해 수행한다.
TDM grooming switch는 대부분의 광역 및 도시 기반 음성/데이터 통신 네트워크에서 핵심적인 역할을 한다. 이러한 네트워크는 일반적으로 SONET ring을 기반으로 구성되며, grooming switch는 여러 ring을 연결하는 cross-connect 또는 느린 전송 채널을 ring에 추가/삭제하는 add-drop multiplexer 역할을 한다.
TDM switch는 일반적으로 보호 이벤트 외에는 구성 변경이 느리다. 새로운 STS-1 회선은 보통 분당 몇 개의 속도로만 설정된다. 하지만 장애(예: 굴착기로 광케이블 절단 등)가 발생하면, VC2002 내의 3,456개 연결 중 많은 수가 수 밀리초 내에 재설정되어야 서비스 중단을 피할 수 있다.
TDM switch는 입력 및 출력 스트림이 시간에 따라 멀티플렉싱된다는 점을 활용하여, Clos 네트워크의 첫 번째 및 세 번째 단계를 시간 도메인에서 구현할 수 있다 (그림 6.21). 이로써 8×8 crossbar의 복잡성을 피하면서 Figure 6.20의 2입력, 4-time slot 예제를 구현할 수 있다.
그림 6.21에서:
- 입력 및 출력 스위치는 4×4 time switch (TSI: Time-Slot Interchanger)로 구현된다.
- 중간 단계의 4개의 2×2 switch는 실제로는 time-multiplexed된 단일 2×2 switch로 구현된다.
TSI는 2n 엔트리의 메모리이다. 입력 스트림이 절반(n개의 엔트리)을 순차적으로 채우는 동안, 다른 절반은 출력 스트림이 임의 순서로 읽는다. 이후 입출력 역할을 바꾸며 반복된다. 이 방식 덕분에 각 time slot에서 middle switch 역할을 하는 단일 2×2 switch로 네 개의 switch를 구현할 수 있다.
그림 6.22는 VC2002의 블록 다이어그램이다. 이 스위치는 다음 구성으로 이루어져 있다:
- 72개의 48×96 입력 TSI
- 72×72 공간 스위치 (96개의 논리적 time slot마다 재구성됨)
- 72개의 96×48 출력 TSI
구성은 현재 time slot 주소를 통해 접근되는 configuration RAM에 의해 제어된다. 각 time slot마다 다음이 정의된다:
- 입력 TSI에서 읽을 위치
- 스위치에서 각 출력 포트에 연결할 입력 포트
- 출력 TSI에서 읽을 위치
이 스위치는 (m, n, r) = (96, 48, 72)의 3단계 TST Clos 네트워크 구조를 따른다. 총 72개의 입력 스트림에 대해 각각 48 time slot이 있으며, 각 입력 스위치에는 96개의 중간 스테이지가 존재하므로 speedup은 2이다. 이로 인해 VC2002는 unicast에 대해 strictly non-blocking, dual-cast(fanout=2)에 대해 rearrangeably non-blocking 특성을 갖는다.
스케줄링 방법은 다음과 같다:
- unicast 트래픽: Figure 6.8의 교집합 방법 또는 Figure 6.11의 looping 알고리즘 사용
- dual-cast 트래픽: Figure 6.16의 greedy 알고리즘 또는 looping 알고리즘을 사용하되, call을 분할하여 라우팅
VC2002는 입력/출력에 SONET framer를 내장하고 있다. 입력 framer는 스트림 정렬과 SONET 오버헤드 처리를 수행하며, 출력 framer는 전송 오버헤드를 생성한다.
또한, 96 time slot을 지원하는 72×72 스위치를 구현하기 위해, 실제로는 두 개의 48-time-slot 스위치를 사용하여 STS-48 byte rate (311MHz)에서 동작하도록 구현된다.
dual-cast call을 두 개의 unicast call로 나누고, 중간 스위치를 두 개의 동일한 부분 집합으로 분할하면, 각 unicast call을 해당 부분 집합에 할당하여 라우팅할 수 있다. 각 부분 집합은 m/2 = n개의 스위치를 가지며, 이 부분 집합 내에서는 unicast call에 대해 rearrangeable 하다.
실제로 VC2002는 Section 6.3.5에서 설명한 방식으로 call을 분할함으로써, 임의의 fanout을 가진 multicast call도 매우 낮은 blocking 확률로 처리할 수 있다. 높은 fanout을 가진 call에 대한 blocking 확률 계산은 연습문제 6.5로 남겨 둔다.
VC2002 하나는 180Gbps의 STS-1 grooming 대역폭을 제공하며, 이는 3,456개의 STS-1 회선을 스위칭할 수 있는 수준이다. 더 큰 grooming switch가 필요할 경우, 여러 개의 VC2002를 Clos 네트워크로 연결할 수 있으며, 그 예가 그림 6.23에 나와 있다.
이 그림은 총 120개의 VC2002를 사용하여 최대 4.3Tbps(1,728 STS-48 또는 82,944 STS-1)를 처리할 수 있는 folded Clos 네트워크를 보여준다.
- 첫 번째 랭크의 72개 칩은 각각 24×48 STS-48 입력 스위치 및 48×24 STS-48 출력 스위치로 동작한다.
- 두 번째 랭크의 48개 칩은 각각 72×72 STS-48 중간 스위치를 구성한다.
이 시스템은 논리적으로 5단계 Clos 네트워크이다. 각 VC2002가 내부적으로 3단계 Clos 구조를 가지므로, 외형상 9단계 네트워크처럼 보일 수 있다. 그러나 실제로는 외부의 TSI만을 고려하여 다음과 같은 TSSST 구조로 해석할 수 있다:
- 48×48 TSI
- 24×48 공간 스위치
- 72×72 공간 스위치
- 48×24 공간 스위치
- 48×48 TSI
경로상의 나머지 네 개의 TSI는 직통(straight-through) 모드로 동작한다. 연습문제 6.6에서는 이 구조를 7단계 TSTSTST 구조로 해석할 수 있는 가능성을 탐색하도록 되어 있다.
이 5단계 논리 네트워크를 스케줄링하려면 다음과 같은 절차를 따른다:
- 중간의 3개 space switch 단계를 48개의 3,456×3,456 space switch로 간주한다 (각 time slot마다 하나).
- (m,n,r) = (48,24,3456) Clos로서, 각 call을 48개 time slot 중 하나에 할당한다.
- 각 time slot에 대해 48개의 물리적 중간 스위치 중 하나에 call을 할당하는 48개의 하위 문제로 나뉜다.
- 각 하위 문제는 (m,n,r) = (48,24,72) Clos로 스케줄링할 수 있다.
6.7 참고문헌 노트
- Clos (1953): non-blocking 네트워크에 대한 최초의 논문 발표, Clos 네트워크 및 strictly non-blocking 조건 제시
- Beneš, Slepian, Duguid: 작은 Clos 네트워크도 rearrangeable 하다는 것을 발견
- König: 이분 그래프의 최대 차수 Δ에 대해 Δ 색으로 간선 색칠(edge coloring)이 가능함을 증명
- Cole: 더 효율적인 간선 색칠 알고리즘 개발
- Waksman: 행렬 분해(matrix decomposition) 관련 연구
- Beneš (1965): rearrangeable non-blocking 네트워크 구현 시 필요한 최소 crosspoint 수의 경계 도출, Beneš 네트워크 소개
- Batcher (1968): 비토닉(bitonic) 정렬 및 Batcher 정렬 네트워크 제안
- Knuth: 정렬 네트워크에 대한 상세한 설명
- Masson and Jordan: Clos 네트워크에서의 multicast 문제 최초 연구
- Yang and Masson: 거의 최적의 multicast 스케줄링 알고리즘 제안
6.8 연습문제
6.1
27포트 Clos. 3×3 crossbar switch를 사용하여 정확히 27개의 포트를 가지는 rearrangeable Clos 네트워크를 설계하시오.
6.2
최대 크기의 Clos 네트워크. n×n crossbar switch를 사용하여 k단계 (k는 홀수)로 구성되는 Clos 네트워크를 만들 때, unicast traffic에 대해 rearrangeable하기 위해 만들 수 있는 최대 포트 수는?
6.3
Looping 알고리즘의 성능. Figure 6.11의 looping 알고리즘을 구현하여 (5,5,5) Clos 네트워크에 대해 실험하시오. 포트가 모두 사용될 때까지 무작위로 connection을 하나씩 추가하며, 각 connection당 평균 몇 번의 재배치가 필요한지 계산하시오. 알고리즘을 수정하여 재배치 횟수를 줄이는 방법도 시도하고, 두 경우의 결과를 비교하여 설명하시오.
6.4
Batcher-banyan 네트워크. Batcher-banyan은 Batcher로 정렬된 call을 banyan(=butterfly)에 전달하는 구조이다. 포트 번호 {aₙ₋₁, ..., a₀}가 Batcher에서 {aₙ₋₂, ..., a₀, aₙ₋₁}로 shuffle 되어 banyan에 전달될 때, 모든 permutation이 blocking 없이 라우팅될 수 있음을 증명하시오.
6.5
확률적 non-blocking multicast. fanout=4인 call이 VC2002 (Section 6.6) 상에서 greedy 알고리즘으로 라우팅될 때, blocking 확률을 추정하시오.
6.6
7단계 time-space switch. Figure 6.23의 120-chip 네트워크를 처음에는 5단계 TSSST로 보았지만, 내부 speedup을 고려하지 않았다. 이제 이 네트워크를 7단계 TSTSTST 구조로 보았을 때, 어떤 트래픽 패턴이 라우팅 가능해지며, 스케줄링에 어떤 영향을 주는지 설명하시오.
6.7
rearrangeability 증명. Hall의 정리를 사용하여 m ≥ n인 Clos 네트워크가 rearrangeable함을 증명하시오.
Hall의 정리
집합 A와 A₁, A₂, ..., Aᵣ가 있을 때, ai ∈ Ai 이며 ai ≠ aj (i ≠ j)를 만족하는 대표자 집합 {a₁, ..., aᵣ}가 존재하려면, 임의의 k개 부분 집합의 합집합 크기가 최소 k 이상이어야 한다.
6.8
Euler 분할을 이용한 그래프 색칠. Euler 분할 기법을 통해 bipartite graph를 edge coloring할 수 있다. 그래프의 모든 간선을 정확히 한 번씩 방문하는 Euler 경로를 찾아, 이를 따라 alternate edge를 서로 다른 두 그래프로 나눈다. 이 과정을 반복하여 차수가 1인 그래프들로 나눈다.
(a) 모든 노드 차수가 2ⁱ일 때, Euler 경로가 항상 존재함을 증명하고, 경로를 찾는 알고리즘을 기술하시오.
(b) 노드 수 V, 차수 2ⁱ인 그래프에서 Euler 분할 기반 색칠 알고리즘의 점근적 수행 시간을 구하고, looping 알고리즘과 비교하시오.
'System-on-Chip Design > NoC' 카테고리의 다른 글
| Routing Basics (1) | 2025.06.02 |
|---|---|
| Slicing and Dicing (1) | 2025.06.02 |
| Torus Networks (2) | 2025.06.02 |
| Butterfly Networks (1) | 2025.06.02 |
| Topology Basics (4) | 2025.06.01 |
