Deadlock and Livelock

zeah 2025. 6. 5. 22:00

2025. 6. 5. 22:00

Deadlock은 interconnection network에서 일반적으로 packet과 같은 여러 agent들이 서로 자원이 해제되기를 기다리며 더 이상 진행할 수 없는 상태를 말한다. 이들 대기 agent들의 순환이 형성되면 네트워크는 deadlock 상태에 빠진다. 간단한 예로 Figure 14.1을 보자. circuit-switched network를 통해 전송 중인 연결 A와 B는 각각 두 개의 channel을 점유하고 있으며, 세 번째 channel을 얻기 전까지는 진행할 수 없다. 하지만 서로 필요한 세 번째 channel은 상대가 점유하고 있어, 어떤 연결도 필요한 channel을 해제할 수 없다. 따라서 두 연결은 deadlock 상태에 빠지며, 외부 개입이 없으면 이 상태는 계속된다. Deadlock은 다양한 자원에 대해 발생할 수 있다. 여기서는 physical channel이지만, virtual channel이나 shared packet buffer에서도 발생 가능하다.

Deadlock은 네트워크에 치명적이다. 일부 자원이 deadlock된 packet들에 점유되면, 다른 packet들이 이 자원을 사용하지 못해 네트워크 전체가 마비될 수 있다. 이를 방지하려면 deadlock avoidance(네트워크가 절대 deadlock되지 않도록 하는 방식)나 deadlock recovery(deadlock 발생 시 이를 탐지하고 복구하는 방식)가 필요하다. 대부분의 현대 네트워크는 deadlock avoidance를 사용하며, 자원에 순서를 부여하고 packet이 이 순서를 따라 자원을 획득하도록 강제한다.

Livelock은 이와 밀접한 네트워크 병리 현상으로, packet이 계속 네트워크를 이동하지만 목적지에 도달하지 못하는 상태이다. 예를 들어 packet이 minimal이 아닌 경로를 허용받을 때 발생할 수 있으며, 이때는 deterministic 또는 probabilistic 방식으로 잘못된 경로 선택 횟수를 제한해야 한다.

14.1 Deadlock

14.1.1 Agent와 Resource

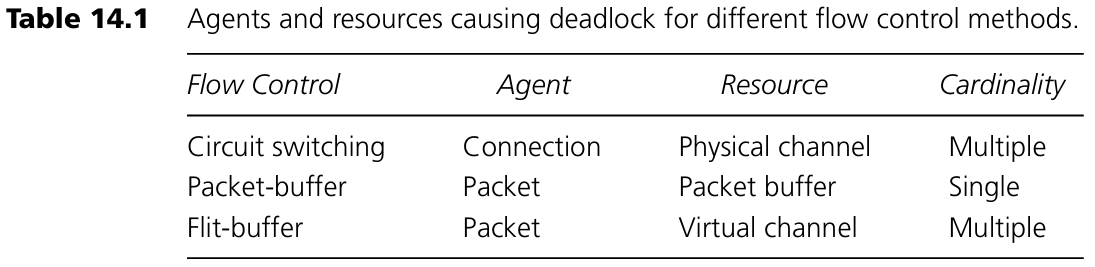
Deadlock에 관여하는 agent와 resource는 사용되는 flow control 방식에 따라 달라진다. Circuit switching의 경우 agent는 connection이고 resource는 physical channel이다. 연결이 설정되면 해당 경로의 모든 channel을 점유하며, 전송이 끝나기 전까지 해제하지 않는다. 따라서 하나의 연결은 여러 개의 channel을 무기한 점유할 수 있다.

Packet-buffer 방식(store-and-forward 또는 virtual cut-through 등)에서는 agent는 packet이며 resource는 packet buffer이다. Packet의 head가 네트워크를 따라 전파되며 각 노드에서 buffer를 획득해야 한다. 이 경우 packet은 한 시점에 하나의 buffer만 점유하며, 새 buffer를 얻은 후 이전 buffer는 일정 시간 내 해제된다.

Flit-buffer 방식에서는 agent는 역시 packet이지만, resource는 virtual channel이다. Packet의 head는 각 노드에서 virtual channel(control state와 flit buffer 포함)을 할당받으며, 여러 개의 virtual channel을 동시에 무기한 점유할 수 있다. 이는 하나의 virtual channel에 packet 전체를 담을 수 없기 때문이다.

14.1.2 Wait-For 관계와 Holds 관계

Agent와 resource는 wait-for 관계와 holds 관계로 연결된다. 예를 들어 Figure 14.1의 경우를 보자. Connection A는 channel u와 v를 점유하고 있고(waits for w), Connection B는 w와 x를 점유한 채(u를 기다림) 대기 중이다. 어떤 agent가 resource를 점유하고 있다면, 이 자원은 해당 agent가 해제해주길 기다리는 상태이다. 따라서 holds(a, b)는 waitfor(b, a)를 의미한다. 이 holds 관계를 반대 방향의 wait-for 관계로 다시 그리면 wait-for 그래프가 된다. Figure 14.2(b)의 사이클이 deadlock 상태임을 보여준다.

이처럼 agent와 resource 간의 엣지가 교차로 연결된 사이클이 존재할 때 deadlock이 발생한다. 즉,

Agent가 어떤 resource를 점유하고 있으면서, 다른 resource를 기다리고 있으며,
이러한 관계가 순환(cycle)을 이루는 경우 (agent A₀가 R₀를 점유하고 R₁을 기다림, A₁이 R₁을 점유하고 R₂를 기다림, ..., Aₙ₋₁이 Rₙ₋₁를 점유하고 R₀을 기다림).

14.1.3 Resource Dependence

Wait-for 그래프에서 두 resource Ri와 Ri+1이 두 칸 떨어져 있다면, agent Ai가 Ri를 점유한 상태에서 Ri+1을 무한히 기다릴 수 있어야 한다. 이를 resource dependence라 하며 Ri → Ri+1 또는 Ri ⇒ Ri+1로 표현한다. Figure 14.1의 예에서는 u → v → w → x → u의 순환 관계가 존재한다. 이 관계는 전이적이며, a → b이고 b → c이면 a → c이다.

Figure 14.3의 resource dependence graph(자원 의존 그래프)는 각 resource가 vertex이며, 의존 관계는 방향 엣지로 표현된다. circuit switching에서는 physical channel 의존 그래프가 되며, packet-buffer 방식에서는 packet-buffer 의존 그래프, flit-buffer 방식에서는 virtual-channel 의존 그래프가 된다.

이러한 resource dependence graph에 사이클이 존재하면 deadlock이 발생할 가능성이 있다. 실제 deadlock이 발생하려면, agent가 자원을 점유하고 동시에 다른 자원을 기다리며 wait-for 그래프에 사이클을 만들어야 한다. 따라서 resource dependence graph의 사이클은 필요조건이지 충분조건은 아니다. Deadlock을 방지하기 위한 일반적인 전략은 이 graph에서 사이클을 제거하는 것이다. 그러면 wait-for 그래프에서 사이클이 생기지 않으며 deadlock도 방지된다.

14.1.4 예시

Figure 14.1의 4-node ring network를 packet-buffer flow control(노드당 하나의 packet buffer)로 바꿔 생각해 보자. 이 경우 agent는 packet이며 resource는 packet buffer이다. Figure 14.4(a)에 packet-buffer dependence graph가 나와 있다. 노드 0의 buffer(B₀)에 있는 packet은 buffer B₁을 얻기 전까지 B₀을 해제하지 않는다. 따라서 B₀ → B₁이라는 의존 관계가 생긴다.

Figure 14.4 설명

(a)는 packet-buffer flow control을 사용하는 네트워크의 resource(=packet buffer) dependence graph이다. 각 노드에 하나씩 있는 packet buffer(B0~B3)는 링 구조에서 다음 buffer를 점유하지 않으면 해제되지 않으므로 B0 → B1 → B2 → B3 → B0이라는 순환이 생긴다.

(b)는 이 상황에서 deadlock이 발생했을 때의 wait-for graph이다. 네 개의 packet(P0~P3)이 각각 하나의 buffer를 점유하고 있으며, 다음 buffer가 비워지기를 기다린다. Packet은 한 번에 하나의 buffer만 점유할 수 있으므로, 이와 같은 4개 packet 구성이 되어야 순환이 생기고 deadlock이 발생할 수 있다.

Flit-buffer flow control 예시 (Figure 14.5)

이제 동일한 4-node ring network를 flit-buffer flow control로 바꾸어 보자. 각 physical channel에 두 개의 virtual channel이 있다고 가정한다. Packet은 다음 채널에서 두 virtual channel 중 하나를 선택하여 대기할 수 있지만, 일단 선택한 channel에 대해 기다리며, 나머지 channel이 비어도 그쪽으로 바꾸지 않는다.

(a)는 각 virtual channel 간의 dependence를 보여주는 graph이며, 인접한 채널 간에는 모두 엣지가 있다.

(b)는 deadlocked 상태를 나타낸 wait-for graph이다. P0은 u0와 v0를 점유하고 w0를 기다리며, P1은 w0와 x0를 점유하고 v0를 기다린다. "1"로 끝나는 virtual channel은 사용되지 않는다. 만약 P0이 w0 또는 w1 중 사용 가능한 것을 선택할 수 있다면, 이 구성은 deadlock이 아니다. 모든 virtual channel 중 아무거나 사용할 수 있는 경우, deadlock 구성을 위해선 4개의 packet이 필요하며, 이는 연습문제로 제시된다.

14.1.5 High-Level (Protocol) Deadlock

Deadlock은 네트워크 외부 요인에 의해 발생할 수도 있다. Figure 14.6을 보자. 위쪽 network channel은 서버가 request packet을 제거해 주기를 기다리고 있는데, 서버는 내부 buffer가 제한되어 있어 reply packet이 먼저 소비되어야 request packet을 수신할 수 있다. 결과적으로 upper channel은 lower channel이 비워지기를 기다리는 셈이며, 이 wait-for 관계는 네트워크 내부가 아니라 서버 외부에 의해 생긴 것이다. 이러한 외부 요인에 포함된 wait-for loop에 의한 deadlock을 high-level 또는 protocol deadlock이라고 한다.

예를 들어 shared-memory multiprocessor에서는 각 노드의 memory server가 memory read/write request를 수신하고 처리 후 응답을 돌려보낸다. 내부 buffer가 제한적이면, Figure 14.6과 같이 서버로 들어오는 채널이 서버에서 나가는 채널을 기다리는 상황이 된다.

이런 외부 wait-for edge의 영향을 없애려면, 요청과 응답을 처리할 때 서로 다른 논리적 네트워크(logical network)를 사용하면 된다. 예: 서로 다른 virtual channel 또는 packet buffer 사용. 특히 cache-coherent 시스템에서는 하나의 transaction이 directory, owner, 다시 directory로 순차적으로 서버를 통과하기 때문에 각 단계마다 분리된 논리 네트워크를 사용하는 것이 일반적이다. 이는 Section 14.2에서 설명할 resource ordering의 특수한 경우이다.

14.2 Deadlock Avoidance

Deadlock은 resource dependence graph에 cycle이 없도록 만들면 방지할 수 있다. 이를 위해 자원에 대해 부분 순서(partial order)를 정의하고, agent가 이 순서를 따르도록 자원을 할당하도록 한다. 이렇게 하면, 순서상 높은 자원을 점유한 상태에서 낮은 자원을 기다리는 것이 금지되므로 cycle이 생기지 않는다. 일반적으로는 자원을 번호로 정렬하여 전체 순서(total order)를 적용한다.

모든 deadlock avoidance 기법은 어떤 형태로든 resource ordering을 사용하지만, 이 ordering이 routing에 미치는 영향은 다양하다. 어떤 방법은 routing에는 제한이 없고, 어떤 방법은 자원 수를 줄이기 위해 특정 경로를 허용하지 않기도 한다.

packet-buffer flow control에서는 노드마다 여러 개의 packet buffer가 있고, flit-buffer flow control에서는 하나의 physical channel에 여러 virtual channel이 있으므로, 동일한 물리 자원 내의 논리 자원에 순서를 부여함으로써 ordering을 구현할 수 있다. 하지만 circuit switching은 물리 채널 자체가 자원이므로, 각 채널이 ordering 내에서 한 위치만 차지할 수 있고, routing 제한이 불가피하다.

14.2.1 Resource Classes

Distance Classes: 자원을 class로 묶어 번호를 붙이고, packet이 자원을 할당할 때 오름차순으로만 접근하도록 제한하는 방식이다. 예: source에서 class 0의 자원을 할당받고, 이후 hop마다 class i+1의 자원만 할당할 수 있도록 한다.

이 시스템에서는 class i의 자원을 점유한 packet은 반드시 class i+1 자원을 기다려야 하므로, resource dependence graph에 cycle이 생기지 않는다. 따라서 deadlock이 발생하지 않는다.

Figure 14.8은 distance 기반 buffer class를 사용하는 4-node ring network의 예다. 각 노드 i는 hop 수 j에 따라 Bji buffer를 갖는다. 이 buffer는 j번 hop을 거친 packet을 수용하고, 다음 node i+1의 Bj+1,i+1로 전송한다. 이 구조는 spiral 형태의 비순환 의존 그래프를 만들어 deadlock을 방지한다.

이러한 "오르막" 자원 할당 규칙을 지키기 위해 packet은 현재 자신이 점유한 class 정보를 기억하고 있어야 한다. 따라서 distance class를 사용하는 경우 routing relation은 다음과 같이 정의된다:

R : Q × N → Q,
여기서 Q는 네트워크 내의 모든 buffer class 집합이다.

flit-buffer 방식에서도 유사하게 virtual channel에 이 방식을 적용할 수 있다. 이 hop-by-hop routing relation은 "오르막" buffer class 사용을 표현한다.

distance class는 어떤 topology에서도 자원 순서를 구현할 수 있는 일반적인 방법이지만, 단점은 네트워크의 지름(diameter)에 비례하는 수의 buffer나 virtual channel이 필요하다는 점이다.

Figure 14.8 설명

Distance class를 4-node ring network에 적용한 예이다. 각 노드 i는 4개의 buffer class를 가지며, buffer Bji는 목적지를 향해 j번 hop을 이동한 packet을 저장한다. 이 구조는 의존 그래프를 비순환적으로 만들기 때문에 deadlock을 방지할 수 있다.

Topology를 활용한 buffer class 최소화

어떤 네트워크에서는 topology를 활용해 필요한 buffer class 수를 크게 줄일 수 있다. 예를 들어, ring network에서는 두 개의 buffer class만으로도 자원을 순서화할 수 있다.

Figure 14.9 설명

Dateline buffer class를 ring에 적용한 예이다. 각 노드 i는 “0” buffer B0i와 “1” buffer B1i를 가진다. source 노드 s에서 주입된 packet은 B0s에 저장되고, dateline(노드 3과 0 사이)을 지날 때까지는 “0” buffer를 계속 사용한다. dateline을 지나면 “1” buffer(B10)를 사용하고 목적지까지 “1” buffer만 이용한다. 이 방식은 원형 의존 구조를 나선형 비순환 구조로 바꾸므로 deadlock을 방지할 수 있다.

Dateline 방식의 flit-buffer 적용 (Figure 14.10)

각 physical channel c는 두 개의 virtual channel c0, c1로 나뉜다. 모든 packet은 처음에 “0” virtual channel을 사용하고, dateline(노드 3)을 지나면 “1” virtual channel로 전환한다. 이때 routing function은 다음과 같은 형식을 가져야 한다:

R : C × N → C,
여기서 C는 virtual channel들의 집합이다.

이렇게 하면 Figure 14.5의 cyclic한 virtual channel dependence graph에서 일부 edge를 제거하여 acyclic하게 만들 수 있다.

Overlapping Resource Classes

distance class나 dateline class를 사용하면 resource dependence graph를 acyclic하게 만들 수 있지만, 부하 불균형(load imbalance)이 발생할 수 있다. 예를 들어 Figure 14.10에서 uniform traffic이 있을 경우, 대부분의 packet이 v0을 사용하고 v1은 거의 사용되지 않게 된다.

이러한 부하 불균형을 줄이기 위한 한 방법은 buffer class를 overlap시키는 것이다. 예를 들어, 32개의 packet buffer가 있을 때, 각 class에 16개씩 할당하는 대신 (Figure 14.11a), 각 class에 독점적인 buffer를 하나씩 두고 나머지 30개는 두 class가 공유하도록 구성할 수 있다 (Figure 14.11b). 이 방식은 대부분의 buffer를 공유함으로써 자원 활용률을 높일 수 있다.

그러나 overlap된 class에서 deadlock을 피하려면 중요한 조건이 있다. packet은 overlap 영역의 busy buffer를 기다려서는 안 된다. 즉, packet은 buffer B11과 같이 두 class가 모두 접근 가능한 buffer에 대해 기다려서는 안 된다. 그렇게 하면 다른 class의 packet과 교착 상태가 될 수 있기 때문이다.

해결 방법은 다음과 같다:

packet은 특정 buffer가 아니라 class 자체에 대해 대기해야 한다.
즉, 해당 class에서 어떤 buffer든 idle 상태가 되기를 기다려야 하며, 독점 buffer가 결국 available해질 것이므로 deadlock은 발생하지 않는다.
만약 공유 buffer가 먼저 비게 된다면 이를 사용해 성능은 향상시킬 수 있다.

14.2.2 Restricted Physical Routes

resource를 class로 구성하여 deadlock을 방지하는 방식은 효과적이지만, 경우에 따라 많은 수의 자원이 필요할 수 있다. 이를 피하기 위한 대안은 routing function을 제한하는 것이다. 적절한 경로 제한을 통해 resource 간의 의존성을 줄이면, 적은 수의 resource class로도 cycle 없는 구조를 만들 수 있다.

Dimension Order (e-cube) Routing

deadlock을 피하기 위한 가장 간단한 routing 제한 중 하나는 k-ary n-mesh에서 dimension-order routing을 사용하는 것이다. 예를 들어 2D mesh에서는 다음과 같은 규칙이 있다:

x 방향으로 +x로 이동 중인 packet은 +x, +y, −y 방향 channel만 대기 가능
−x 방향 packet은 −x, +y, −y만 대기 가능
y 방향에서는 +y는 +y만, −y는 −y만 대기 가능

이러한 제약을 기반으로 network의 channel을 나열하면 deadlock이 발생하지 않는다.

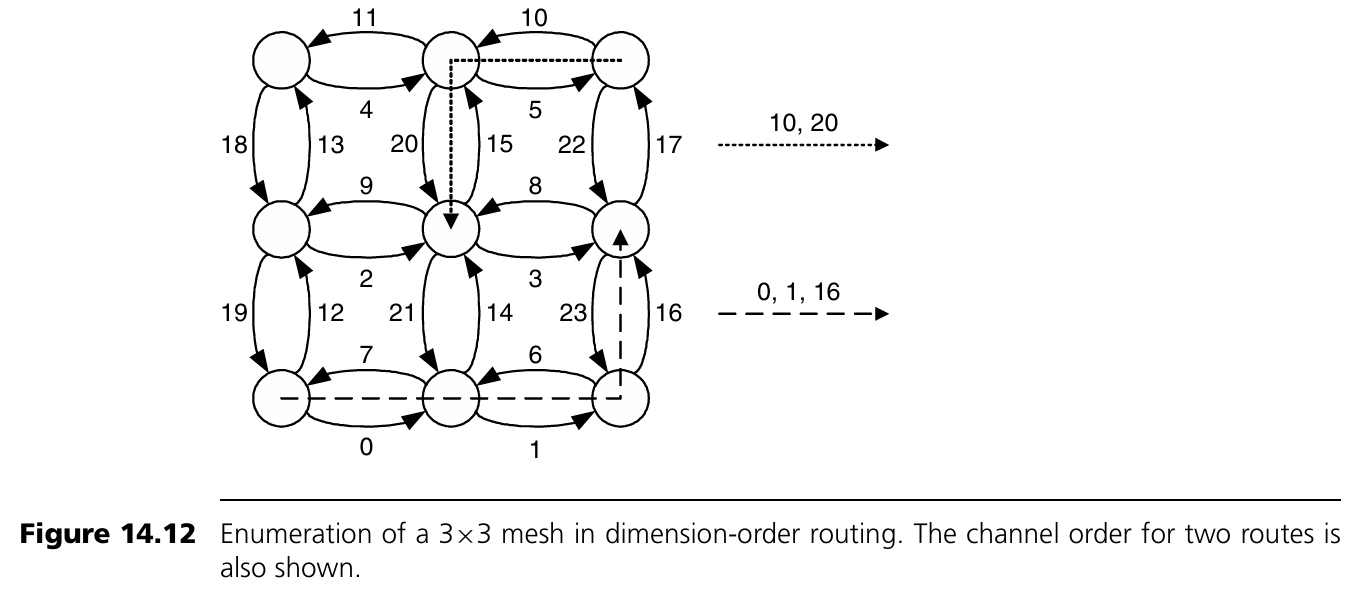
Figure 14.12 설명

3×3 mesh에서 dimension-order routing을 위한 channel numbering 예이다. 오른쪽 방향 channel을 먼저 나열하고, 그다음 왼쪽, 위, 아래 방향 순서로 번호를 매긴다. 이 방식은 routing 경로가 증가하는 번호의 channel을 따라가도록 보장하며, deadlock을 피할 수 있게 한다.

Turn Model

Dimension-order routing은 k-ary n-mesh network에서 deadlock 방지를 위한 routing 제약의 한 방식이지만, turn model은 mesh network에서 routing 알고리즘을 제약하는 좀 더 일반적인 프레임워크를 제공한다. turn model에서는 deadlock cycle을 구성하는 데 필요한 특정 방향 전환(turn)에 대해 정의하며, 2차원 예제로 설명이 시작된다.

Figure 14.13 설명 – Turn Model

(a) 2차원 mesh network에서 8개의 가능한 turn(예: +x → +y, +x → -y 등)이 있고, 이를 두 개의 추상적인 cycle로 나눌 수 있다. Deadlock을 피하려면 이 두 cycle 각각에서 최소 하나의 turn을 제거해야 한다.

(b) 예를 들어, +y → -x turn(North to West)을 제거하면 첫 번째 cycle을 깨뜨릴 수 있다.

West-first routing: South → West turn 제거. Packet은 West 방향으로 먼저 모두 이동한 뒤, 그 이후 다른 방향으로 이동 가능.
North-last routing: North → East turn 제거. Packet은 North 방향을 제외한 다른 방향으로 자유롭게 이동 가능하지만, North로 들어선 후엔 계속 North로만 이동.
Negative-first routing: East → South turn 제거. Packet은 South와 West 방향으로 먼저 이동한 후, North와 East 방향으로 이동.

이러한 turn 제한은 결국 resource ordering을 다르게 정의하는 것이며, dimension-order routing과 마찬가지로 total order를 만든다. Figure 14.14는 west-first routing이 적용된 3×3 mesh의 channel 순서를 보여준다.

Turn Model과 Dimension-Order Routing의 한계

이러한 deadlock-free routing 기법들은 routing 경로의 다양성을 줄여 네트워크 성능과 fault tolerance에 영향을 줄 수 있다. 특히 dimension-order routing은 경로 다양성을 0으로 만든다. 또한 torus와 같은 topology에서는 channel cycle을 제거할 수 없다.

14.2.3 Hybrid Deadlock Avoidance

지금까지의 방법은 자원을 나누고 번호를 부여하거나, routing path를 제한하여 deadlock을 피하는 방식이었지만 각각 단점이 있었다:

Buffer class 방식: 노드당 많은 buffer 필요
Routing 제한 방식: 경로 다양성 감소, 모든 topology에 적용 불가

현실적인 해결책은 두 방식을 혼합하는 것이다.

Torus Routing에서의 Hybrid 기법

Torus network에서는 각 dimension에 dateline class를 적용하고, 그 위에 dimension-order routing을 적용하면 deadlock을 피할 수 있다. dateline class가 torus를 mesh처럼 동작하도록 만들어주기 때문이다.

예: flit-buffer flow control에서는 각 physical channel에 두 개의 virtual channel을 둔다. Packet은 처음엔 virtual channel 0을 사용하고, 각 dimension의 dateline을 통과하면 virtual channel 1로 전환된다. 다음 dimension으로 넘어갈 때는 항상 다시 virtual channel 0에서 시작한다.

이처럼 virtual channel을 이용해 의존성을 끊고 다시 연결하는 방식은 다양한 상황에 일반화 가능하다.

예를 들어 Section 14.1.5에서 설명한 protocol deadlock에서도, 요청과 응답을 서로 다른 virtual channel로 분리하여 해결할 수 있다. underlying routing이 deadlock-free라면, request-reply protocol 자체가 deadlock을 만들지 않게 된다.

Planar-Adaptive Routing

이 기법은 virtual channel과 restricted physical route를 결합한 것으로, 제한된 adaptivity를 허용하면서도 channel dependence graph의 cycle을 방지한다.

k-ary n-mesh에서 두 개의 인접 dimension (i, i+1)을 adaptive plane으로 정의
각 plane에서는 minimal adaptive routing을 허용
plane 수는 n-1개이고, routing은 plane A₀ → A₁ → … → Aₙ₋₂ 순으로 진행

Figure 14.15 설명

(a) k-ary 3-mesh에서 source와 destination 간 가능한 모든 minimal path
(b) Planar-adaptive routing으로 허용된 path의 subset

이 방식은 network 크기나 dimension 수에 관계없이 virtual channel 수를 일정하게 유지하며, 경로 다양성은 상당 수준 확보된다.

Virtual Channel 구조

각 채널은 세 개의 virtual channel로 나뉘고, 각각은 di,v로 표시된다. 여기서 i는 dimension, v는 virtual channel ID.

Plane Ai는 di,2, di+1,0, di+1,1을 포함
Routing은 Ai에서 시작해, i번째 dimension이 목적지와 일치하면 다음 plane으로 이동
마지막 dimension까지 routing 후 packet은 목적지에 도달

deadlock-free를 보장하기 위해 각 plane 내의 virtual channel은 증가 방향과 감소 방향으로 나뉜다:

증가 방향: di,2⁺, di+1,0
감소 방향: di,2⁻, di+1,1

packet은 증가가 필요하면 증가 방향 채널만 사용하고, 감소 시에는 감소 방향 채널만 사용한다.

14.3 Adaptive Routing

앞 절까지는 resource dependence graph에서 cycle을 제거하여 deadlock을 막는 구조였으며, 일부는 adaptive routing algorithm으로 자연스럽게 표현할 수 있다.

예:

west-first routing은 packet이 west 방향으로 이동할지 여부를 network 상황에 따라 adaptive하게 결정할 수 있다.
일부 buffer class 기반 방법도 adaptive 요소를 포함할 수 있다.

그러나 이 절의 초점은 다음의 중요한 차이에 있다:

Adaptive routing은 cyclic resource dependence graph를 허용하면서도 deadlock-free가 될 수 있다.

이 개념은 path 다양성 감소 없이도 deadlock을 피할 수 있게 해 준다.

14.3.1 Routing Subfunctions and Extended Dependences

deadlock-free를 유지하면서도 cycle이 있는 dependence graph를 허용할 수 있는 핵심 아이디어는 다음과 같다:

모든 potential cycle에 대해 escape path를 제공하는 것이다.

즉, packet이 cycle에 갇힐 상황이 되어도, 탈출 가능한 deadlock-free 경로가 존재한다면 전체 네트워크는 deadlock-free 상태로 유지된다.

예제: 2D Mesh에서의 Escape Path 기반 Routing

flit-buffer flow control을 사용하고, 각 physical channel에 2개의 virtual channel을 둔 2D mesh를 예로 들어보자. channel은 xydv 형태로 표현되며, 이는 노드, 방향, virtual channel class를 의미한다. 예: 10e0는 node 10의 east 방향 virtual channel class 0이다.

Routing 규칙은 다음과 같다:

모든 routing은 minimal이어야 한다.
class 1의 virtual channel(xyd1)은 어떤 방향의 어떤 class로도 route 가능
class 0의 virtual channel(xyd0)은 목적지에서 class 1으로만 route 가능
class 0의 virtual channel은 dimension order(x 먼저, 그다음 y)로만 class 0으로 route 가능

즉, source나 destination 중 하나라도 class 1이면 자유롭게 route 가능하지만, 둘 다 class 0이면 dimension order만 허용된다.

Figure 14.16은 위 규칙을 따르는 네 개 노드에 대한 virtual channel dependence graph를 보여준다. 00e0 → 10n0 → 11w1 → 01s1 → 00e0 의 cycle이 존재하지만, 각 packet은 escape path를 통해 cycle을 회피할 수 있다.

예를 들어 packet A는 00e0과 10n0을, packet B는 11w1과 01s1을 점유하고 있다고 하자. 만약 A가 11w1을 기다리고, B가 00e0을 기다리면 deadlock이 될 수 있다. 하지만 A는 11n0으로 route 가능하므로 escape path가 존재한다. 이러한 escape 경로가 있는 한, 그리고 packet이 busy 자원에 대해 기다리지 않는다면, deadlock은 발생하지 않는다.

Indirect Dependence

만약 규칙 1(minimal routing)이 없고 non-minimal routing이 허용된다면, indirect dependence에 의해 escape path에서도 cycle이 발생할 수 있다.

예를 들어 Figure 14.16에서 packet A가 00e0을 점유하고, packet B가 non-minimal 경로를 따라 10n0 → 11w1 → 01s1 을 점유하면, B는 00e0을 요구하게 되어, 00e0 → 10n0 → 11w1 → 01s1 → 00e0 형태의 indirect cycle이 형성된다.

이런 경우, escape path가 더 이상 deadlock-free를 보장하지 못한다.

해결 방법: escape channel 간에는 명시적인 순서를 부여하고, b ≼ a 인 escape channel로는 route를 금지한다. 예: class 1의 route는 minimal하게 제한함으로써 indirect dependence를 차단할 수 있다.

참고로, indirect dependence 문제는 flit-buffer flow control에서만 발생하며, packet-buffer flow control에서는 packet이 한 번에 하나의 buffer만 점유하므로 해당되지 않는다.

형식적 정의: Extended Dependence Graph

Adaptive routing을 위한 형식적인 deadlock-free 조건:

전체 routing relation R : C × N → P(C)
escape routing subrelation R₁ ⊆ R, 해당 채널 집합 C₁ ⊆ C
R₁은 connected하고, extended dependence graph에 cycle이 없어야 함
나머지 routing 관계는 Rᶜ = R − R₁

Extended Dependence Graph 정의:

vertex: C₁에 속한 virtual channel
edge:
- direct dependence: ci → cj, if cj ∈ R₁(ci, x)
- indirect dependence: ci → cj, 경로가 R₁ → Rᶜ(하나 이상) → R₁로 이어질 경우 발생

예: Figure 14.16에서 non-minimal 경로를 따라간 경우 indirect dependence가 발생

간단한 해결책: R₁에서 Rᶜ로의 전환을 금지하면 indirect dependence가 제거됨

Theorem 14.1 (Duato의 정리)

adaptive routing relation R이 deadlock-free가 되기 위한 조건:

연결된 routing subrelation R₁이 존재하고, R₁의 extended dependence graph에 cycle이 없다면 R은 deadlock-free이다.

이 정리는 wormhole flow control뿐 아니라 store-and-forward, cut-through network에도 적용된다. store-and-forward에서는 packet이 여러 채널을 동시에 점유할 수 없기 때문에 indirect dependence가 사라지고, direct dependence만 고려하면 된다.

14.3.2 Duato’s Protocol for Deadlock-Free Adaptive Algorithms

Duato의 정리는 이론적 기반을 제공하지만, 이를 실제 network 설계에 적용하는 구체적인 방법은 아래와 같다.

Duato의 프로토콜은 세 단계로 구성된다:

기반 네트워크 설계: deadlock-free가 되도록 설계한다. 예: torus에서는 virtual resource를 추가해 cycle 제거
virtual resource 확장: 각 physical resource에 새로운 virtual resource를 추가한다.
- wormhole: virtual channel
- store-and-forward: buffer
  기존 virtual resource는 escape routing(R₁)을, 새로운 virtual resource는 일반 routing(Rᶜ)을 담당
flow control에 따른 제한:
- packet-buffer flow control: Rᶜ에 제한 없음
- flit-buffer flow control: R₁의 extended dependence graph가 acyclic해야 함

Duato의 방식은 보통 R₁을 dimension-order routing으로 설정하여 minimal adaptive routing 알고리즘을 구현하는 데 사용된다. 예를 들어, 3-ary 2-mesh에서 wormhole flow control과 함께 dimension-order routing을 escape path로 설정할 수 있다.

14.4 Deadlock Recovery

앞서 살펴본 방법들은 deadlock이 발생하지 않도록 사전에 방지하는 방식이었다. 이러한 방법은 routing 제약이나 자원 추가를 통해 cyclic dependence를 제거한다. 그러나 또 다른 접근법은 deadlock을 회피하지 않고, 발생 후 복구하는 것이다. 추가 자원 확보가 어렵거나 routing 제약에 따른 성능 저하가 우려되는 경우 이 접근법이 유리할 수 있다. 물론 deadlock이 드물게 발생하고 평균 성능이 중요할 때 적절하다.

deadlock recovery는 크게 두 단계로 나뉜다:

탐지(detection): 네트워크가 deadlock 상태인지 판단
복구(recovery): deadlock을 해제

탐지를 위해 wait-for graph 내 cycle을 찾는 것은 어렵고 비용이 크므로, 현실적 시스템에서는 보수적 탐지 방식을 사용한다. 보수적 탐지는 실제 deadlock인 경우는 반드시 탐지하지만, deadlock이 아닌 상태도 잘못 탐지할 수 있다(false positive). 일반적으로 timeout counter를 통해 구현한다. 각 자원에 counter를 설정하고, 전송이 발생하면 리셋한다. 일정 시간 동안 전송이 없으면 deadlock으로 간주하고 복구 단계를 시작한다.

14.4.1 Regressive Recovery

Regressive recovery에서는 deadlock된 packet이나 connection을 네트워크에서 제거한다.

예:

circuit switching: 부분적으로 설정된 연결들 중 cycle을 형성한 경우 timeout이 초과되면 관련 연결을 해제하고 재시도한다.
compressionless routing (wormhole 기반): flit이 끝까지 전송될 때까지 timeout을 측정하고, 시간 초과 시 해당 packet을 제거하고 재전송한다. 이를 위해 padding flit을 덧붙여 head가 목적지에 도달했음을 보장한다.

단점: 짧은 packet이 많을 경우 padding이 과도하게 들어가 throughput이 저하된다.

14.4.2 Progressive Recovery

Progressive recovery는 packet을 제거하지 않고 deadlock을 해제한다. 자원 낭비 없이 높은 성능을 기대할 수 있고, 반복 전송으로 인한 livelock 위험도 없다.

예: DISHA 아키텍처

각 노드에 shared escape buffer를 둠
suspected deadlock 상황이 감지되면 해당 buffer를 통해 packet을 drain
escape buffer는 deadlock-free routing sub-function에 의해 동작

Duato의 방식이 하드웨어로 구현된 예다. virtual channel이나 buffer가 값비싼 자원인 시스템에서는 이 접근이 유리하지만, 어떤 시스템에서는 shared buffer 도입 자체가 더 비쌀 수 있다.

14.5 Livelock

Livelock은 packet이 계속 움직이지만 목적지에 도달하지 못하는 상태이다. non-minimal routing에서 misroute 제한이 없으면 무한히 돌아다닐 수 있다. 또한 dropping flow control에서도 재입장 시마다 packet이 버려지면 목적지 도달이 불가능하다.

해결 방법:

Deterministic avoidance: packet에 misroute 횟수 또는 age 기반 priority를 부여
- misroute count가 임계값에 도달하면 더 이상 misroute 불가
- age priority 방식은 일정 시간이 지나면 packet이 가장 높은 우선순위를 가지므로 도달 가능
Probabilistic avoidance: packet이 T 사이클 동안 네트워크에 남아있을 확률이 T → ∞일 때 0으로 수렴하도록 설계
- 예: 2-ary k-mesh, deflection routing, 단일 flit packet의 경우
  최대 이동 거리 Hmax = 2(k−1)
  history string에서 목적지 방향 이동 횟수 t와 deflection 횟수 d의 차이가 Hmax를 넘으면 도달 보장
  목적지 방향으로의 routing 확률이 항상 0보다 크다면, 결국 도달 확률은 1에 수렴

14.6 Case Study: Cray T3E에서의 Deadlock Avoidance

Cray T3E는 T3D의 후속 모델로, Alpha 21164 프로세서를 기반으로 최대 2,176개의 노드까지 확장 가능하다. topology는 3D torus이며, 기본적으로 8×32×8 3-cube로 구성되어 2,048개의 노드를 포함하며, 나머지는 redundancy 및 운영 체제 노드로 구성된다.

주요 설계 특징:

T3E router는 CMOS ASIC으로 구현되어 ECL 기반보다 느리지만 latency 허용폭 증가로 보완
adaptive routing을 사용하여 T3D의 dimension-order routing보다 throughput 향상 및 fault-tolerance 개선
Duato의 protocol 적용
- cut-through flow control 사용
- 각 노드에는 최대 길이 packet을 저장할 수 있는 충분한 buffer 보유
- 따라서 indirect dependence가 존재하지 않음 → routing sub-function이 deadlock-free면 전체도 deadlock-free

Routing sub-function: Direction-order routing

+x → +y → +z → -x → -y → -z 순서
packet header의 3비트를 통해 각 방향의 증가/감소 여부 지정
+에서 −로는 전환 가능하나, −에서 +로는 불가 → mesh에서 deadlock 없음

Fault tolerance 향상 기법

Initial hop: 시작 시 어느 증가 방향으로든 이동 가능
Final hop: 모든 이동 후 −z 방향 허용
Figure 14.18에서 faulty link를 우회하여 패킷이 목적지 도달 가능

Torus에서의 Deadlock 방지: Dateline 방식

각 dimension에 dateline 지정
dateline을 넘는 packet은 VC0에서 시작해 dateline 이후 VC1로 전환
dateline을 넘지 않는 packet은 VC0 또는 VC1 중 하나 선택
VC 선택은 부하 균형을 목표로 최적화
- 특정 physical channel의 VC별 packet 수를 균형 맞춤
- Simulated annealing 기법으로 VC assignment 최적화 수행

Figure 14.18 설명

Figure 14.18은 direction-order routing 전에 initial hop을 허용함으로써 fault-tolerance가 어떻게 향상되는지를 보여준다. 회색 경로는 기본 direction-order routing이며, faulty channel(X 표기)을 통과한다. 그러나 −y 방향으로 initial hop을 한 후 우회 경로(굵은 선)를 통해 node 20에서 node 03으로 도달할 수 있다.

T3E의 virtual channel 구성 요약

2개 VC: torus 내 각 dimension의 dateline deadlock 방지
2개 VC: request / reply message용 별도 virtual network 구성 (high-level deadlock 방지)
1개 VC: minimal adaptive routing용
→ 총 5개 virtual channel이 T3E에서 사용됨

14.7 Bibliographic Notes

초기 deadlock-free 네트워크 연구에서는 자원을 번호 매겨 순서대로 접근하는 방식이 제안됨
Linder와 Harden은 차원이 늘어날수록 필요한 virtual channel 수가 지수적으로 증가하는 adaptive routing deadlock-free 방법을 개발
Glass와 Ni는 제한된 adaptivity를 허용하면서도 deadlock-free인 turn model을 제안
Dally와 Aoki는 일부 non-minimal 경로와 제한된 dimension reversal을 허용하는 방법 제안
Duato는 extended channel dependence graph를 도입하고, deadlock-free adaptive routing을 위한 이론을 확립
- 이 방법은 Cray T3E, Reliable Router, Alpha 21364 등에 적용됨
Planar adaptive routing은 제한된 자원으로 deadlock-free를 달성할 수 있는 구체적 예시
Irregular topology에서는 up*/down* 알고리즘이 사용되며, DEC AutoNet에 적용된 바 있음
Compressionless routing은 circuit switching 개념을 응용한 deadlock recovery 방식으로, Kim 등이 제안
DISHA는 Duato 기반의 하드웨어 복구 방식
VC 불균형 문제는 torus에서 특히 문제가 되며, Cray는 simulated annealing으로 VC 할당을 최적화함

14.8 Exercises (연습 문제 안내)

몇 가지 주요 연습문제 설명:

14.1: Figure 14.5의 네트워크에서 어떤 VC든 먼저 비는 쪽으로 선택 가능한 경우 deadlock configuration의 wait-for graph를 그려라.
14.2: 여러 oblivious routing 알고리즘이 deadlock-free인지 판단. channel dependence graph를 분석.
14.3: Figure 14.13(c)의 네 번째 turn 제거 방식이 왜 deadlock-free가 아닌지 설명.
14.4: turn model로 deadlock-free를 보장하려면 최소 몇 개의 turn을 제거해야 하는지 하한선 도출.
14.6: ring에서 dateline 방식의 virtual channel 불균형 문제를 해결하는 deadlock-free routing 알고리즘 설계.
14.7: planar adaptive routing이 k-ary n-mesh에서 deadlock-free임을 증명.
14.8: Fault-tolerant planar adaptive routing (FPAR)의 두 가지 case 분석을 통해 plane 간과 내부에서 deadlock-free를 보장하는지 검증.
14.9: Cray T3E의 direction-order routing이 deadlock-free임을 채널 나열로 증명하고, initial/final hop 확장이 deadlock-free인지 추가 검증.
14.10: dimension traversal 순서가 완전히 랜덤인 routing에서 n! VC 대신 적은 수로 deadlock-free를 유지할 수 있는 방법 찾기.
14.11: multi-flit packet이 있는 deflection routing에서는 probabilistic 방식이 livelock-free를 보장하지 않는 이유 설명.

'System-on-Chip Design > NoC' 카테고리의 다른 글

Router Architecture (2)	2025.06.05
Quality of Service (1)	2025.06.05
Buffered Flow Control (1)	2025.06.05
Flow Control Basics (2)	2025.06.02
Routing Mechanics (2)	2025.06.02

Zeah Engineering Factory